تحليل التباين هو مجموعة من الطرق الإحصائية المصممة لاختبار الفرضيات حول العلاقة بين علامات معينة والعوامل التي تجري دراستها ، والتي لا تحتوي على وصف كمي ، وكذلك لتحديد درجة تأثير العوامل وتفاعلها. في الأدب المتخصص ، غالبًا ما يطلق عليه ANOVA (من الاسم الإنجليزي تحليل الاختلافات). تم تطوير هذه الطريقة لأول مرة بواسطة R. Fisher في عام 1925.
أنواع ومعايير تحليل التباين
تستخدم هذه الطريقة لدراسة العلاقة بين السمات النوعية (الاسمية) والمتغير الكمي (المستمر). في الواقع ، يختبر الفرضية القائلة بأن الوسط الحسابي للعديد من العينات متساوي. وبالتالي ، يمكن اعتباره معيارًا حدوديًا لمقارنة مراكز عدة عينات في وقت واحد. إذا استخدمت هذه الطريقة لعينتين ، فستكون نتائج تحليل التباين مطابقة لنتائج اختبار t-student. ومع ذلك ، بخلاف المعايير الأخرى ، تتيح لنا هذه الدراسة دراسة المشكلة بمزيد من التفاصيل.

يعتمد تحليل التباين في الإحصائيات على القانون: مجموع مربعات الانحرافات للعينة المدمجة يساوي مجموع مربعات انحرافات intragroup ومجموع مربعات انحرافات intergroup. بالنسبة للدراسة ، يتم استخدام اختبار Fisher لتحديد أهمية الفرق بين الفروق بين المجموعات من الفروق داخل المجموعة. ومع ذلك ، من أجل هذا ، فإن المتطلبات الأساسية الضرورية هي التوزيع الطبيعي والمثلية الجنسية (المساواة في الفروق) للعينات. التمييز بين تحليل التباين أحادي البعد (أحادي المتغير) والمتعدد المتغيرات (متعدد المتغيرات). الأولى تدرس اعتماد الكمية المدروسة على سمة واحدة ، والثانية - فورًا على الكثيرين ، وتتيح لك أيضًا تحديد العلاقة بينهما.
العوامل
تسمى العوامل الظروف الخاضعة للرقابة التي تؤثر على النتيجة النهائية. يطلق على مستواها أو طريقة معالجتها القيمة التي تميز المظهر المحدد لهذا الشرط. عادة ما يتم تقديم هذه الأرقام بمقياس رمزي أو تسلسلي. في كثير من الأحيان ، يتم قياس قيم الخرج في المقاييس الكمية أو الترتيبية. ثم تنشأ مشكلة تجميع بيانات المخرجات في سلسلة من الملاحظات ، والتي تقابل نفس القيم العددية تقريبًا. إذا كان عدد المجموعات كبيرًا جدًا ، فقد يكون عدد الملاحظات فيها غير كافٍ للحصول على نتائج موثوقة. إذا كنت تأخذ الرقم صغيرًا جدًا ، فقد يؤدي ذلك إلى فقدان ميزات هامة للتأثير على النظام. تعتمد الطريقة المحددة لتجميع البيانات على حجم وطبيعة التباين في القيم. غالبًا ما يتم تحديد عدد الفواصل الزمنية وحجمها في التحليل أحادي الاتجاه من خلال مبدأ الفواصل الزمنية المتساوية أو مبدأ الترددات المتساوية.
تحليل مشاكل التباين
لذلك ، هناك حالات عندما تحتاج إلى مقارنة عينتين أو أكثر. عندها يُنصح باستخدام تحليل التباين. يشير اسم الطريقة إلى أن الاستنتاجات مستمدة من دراسة مكونات التباين. جوهر الدراسة هو أن التغيير العام في المؤشر ينقسم إلى أجزاء مكونة تتوافق مع عمل كل عامل على حدة. النظر في عدد من المشاكل التي يحلها تحليل نموذجي من التباين.
مثال 1
تحتوي ورشة العمل على عدد من الأدوات الآلية - الآلات الأوتوماتيكية التي تنتج جزء معين. حجم كل جزء هو قيمة عشوائية ، والتي تعتمد على إعدادات كل آلة والانحرافات العشوائية التي تحدث أثناء تصنيع الأجزاء.من الضروري تحديد ما إذا كانت الآلات قد تم تكوينها بالتساوي وفقًا لقياسات أبعاد الأجزاء.
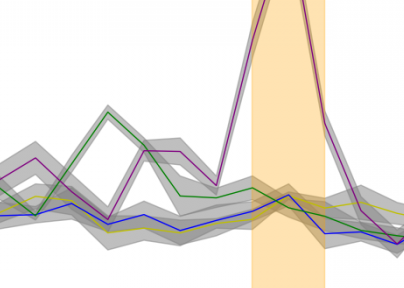
مثال 2
أثناء تصنيع الجهاز الكهربائي ، يتم استخدام أنواع مختلفة من الورق العازل: مكثف ، كهربائي ، إلخ. يمكن تشريب الجهاز بمواد مختلفة: راتنجات الإيبوكسي ، الورنيش ، راتنجات ML-2 ، إلخ. يمكن القضاء على التسربات تحت ضغط عالٍ ، بالتسخين. يمكن تشريبها عن طريق الغمر في الورنيش ، تحت دفق مستمر من الورنيش ، إلخ. يتم سكب الجهاز الكهربائي ككل بمركب معين ، والذي توجد به عدة خيارات. مؤشرات الجودة هي القوة العازلة للعزل ، ودرجة حرارة ارتفاع درجة حرارة اللف في وضع التشغيل ، وعدد آخر. أثناء اختبار العملية التكنولوجية لأجهزة التصنيع ، من الضروري تحديد كيفية تأثير كل عامل من العوامل المدرجة على أداء الجهاز.
مثال 3
يخدم مستودع ترولي باص عدة طرق ترولي باص. تعمل أنواع مختلفة من عربات النقل الخاصة بهم ، ويتم جمع رسوم الأجرة من خلال 125 وحدة تحكم. تهتم إدارة المستودع بالسؤال التالي: كيف يمكن مقارنة الأداء الاقتصادي لكل وحدة تحكم (إيرادات) مع مراعاة الطرق المختلفة والأنواع المختلفة من حافلات العربات؟ كيفية تحديد الجدوى الاقتصادية للإفراج عن نوع معين من العربات على طريق معين؟ كيفية تحديد متطلبات معقولة لمقدار الإيرادات التي يجلبها الموصل في كل مسار في أنواع مختلفة من حافلات العربات؟
تتمثل مهمة اختيار إحدى الطرق في كيفية الحصول على أقصى قدر من المعلومات المتعلقة بالتأثير على النتيجة النهائية لكل عامل ، وتحديد الخصائص العددية لهذا التأثير ، وموثوقيتها بأقل تكلفة وفي أقصر وقت ممكن. حل مثل هذه المشاكل تسمح بطرق تحليل التباين.
تحليل في اتجاه واحد
تهدف الدراسة إلى تقييم حجم تأثير حالة معينة على المراجعة التي تم تحليلها. قد تتمثل مهمة أخرى للتحليل أحادي الاتجاه في مقارنة حالتين أو أكثر ببعضها البعض من أجل تحديد الفرق في تأثيرها على الاستعادة. إذا تم رفض الفرضية الصفرية ، فستكون الخطوة التالية هي التقييم الكمي وبناء فواصل الثقة للخصائص التي تم الحصول عليها. في حالة متى فرضية لاغية لا يمكن إهمالها ، وعادة ما يتم قبولها ويتم التوصل إلى استنتاج حول جوهر التأثير.
يمكن أن يتحول التحليل أحادي المتغير إلى تماثل غير باراميتري لطريقة ترتيب Kraskel-Wallis. تم تطويره من قبل عالم الرياضيات الأمريكي وليم كراسكل والخبير الاقتصادي ويلسون واليس في عام 1952. تم تعيين هذا المعيار لاختبار الفرضية الفارغة وهي أن التأثيرات على العينات المدروسة متساوية مع قيم متوسط غير معروفة ولكنها متساوية. يجب أن يكون عدد العينات أكثر من اثنين.

تم اقتراح معيار Jonkhier (Jonkhier-Terpstra) بشكل مستقل من قبل عالم الرياضيات الهولندي T.J. Terpstrom في عام 1952 والعالم النفسي البريطاني E.R Jonkhier في عام 1954. يتم استخدامه عندما يكون معروفًا مسبقًا أن مجموعات النتائج المتاحة مرتبة حسب نمو تأثير العامل المدروس ، والذي يقاس على نطاق ترتيبي.
يستخدم اختبار بارتليت ، الذي اقترحه الإحصائي البريطاني موريس ستيفنسون بارتليت في عام 1937 ، لاختبار الفرضية الصفرية حول مساواة الفروق بين العديد من المجموعات السكانية العامة العادية التي أخذت منها العينات ، وبصفة عامة أحجام مختلفة (يجب أن يكون عدد كل عينة أربعة على الأقل) ).
G هو اختبار Cochren ، الذي اكتشفه الأمريكي William Gemmel Cochren في عام 1941. وهو يستخدم لاختبار الفرضية الفارغة وهي أن الفروق بين عامة السكان العاديين متساوية في العينات المستقلة ذات الحجم المتساوي.
يعد معيار ليفين اللامعلمي ، الذي اقترحه عالم الرياضيات الأمريكي هوارد ليفين عام 1960 ، بديلاً لمعيار بارتليت في الظروف التي لا يوجد فيها يقين بأن العينات المدروسة تطيع التوزيع الطبيعي.
في عام 1974 ، اقترح الإحصائيون الأمريكيون مورتون ب. براون وألان ب. فورسيث إجراء اختبار (معيار براون فورسيث) ، والذي يختلف إلى حد ما عن معيار لوفين.
تحليل عاملين
يستخدم تحليل التباين ثنائي الاتجاه للعينات الموزعة بشكل طبيعي. في الممارسة العملية ، غالبًا ما تستخدم الجداول المعقدة لهذه الطريقة ، خاصة تلك التي تحتوي كل خلية فيها على مجموعة من البيانات (قياسات متكررة) تقابل قيم المستوى الثابت. إذا لم يتم الوفاء بالافتراضات اللازمة لتطبيق تحليل التباين في اتجاهين ، فسيتم استخدام معيار رتبة فريدمان غير المعلمي (فريدمان ، كيندال وسميث) الذي وضعه الاقتصادي الأمريكي ميلتون فريدمان في نهاية عام 1930. هذا المعيار مستقل عن نوع التوزيع.
من المفترض فقط أن توزيع الكميات هو نفسه ومستمر ، وأنها مستقلة عن بعضها البعض. عند اختبار الفرضية الصفرية ، يتم تقديم الإخراج في شكل مصفوفة مستطيلة تتوافق الصفوف مع مستويات العامل B وتتوافق الأعمدة مع مستويات A. يمكن أن تكون كل خلية من الجدول (كتلة) نتيجة لقياسات المعلمات على كائن واحد أو على مجموعة من الكائنات بقيم ثابتة لمستويات كلا العاملين . في هذه الحالة ، يتم توفير البيانات المقابلة باعتبارها القيم المتوسطة لمعلمة معينة لجميع القياسات أو كائنات العينة المدروسة. لتطبيق معيار بيانات المخرجات ، من الضروري التبديل من نتائج القياس المباشر إلى رتبتها. يتم تنفيذ الترتيب لكل صف على حدة ، أي أن القيم مرتبة لكل قيمة ثابتة.

يهدف معيار الصفحة (المعيار L) ، الذي اقترحه الإحصائي الأمريكي E. B. Page في عام 1963 ، إلى اختبار الفرضية الفارغة. بالنسبة للعينات الكبيرة ، يتم استخدام تقريب الصفحة. إنهم ، وفقًا لواقع الفرضيات الفارغة المقابلة ، يطيعون التوزيع الطبيعي القياسي. في حالة احتواء صفوف الجدول المصدر على نفس القيم ، من الضروري استخدام متوسط الرتب. علاوة على ذلك ، ستكون دقة الاستنتاجات أسوأ ، وكلما زاد عدد هذه المصادفات.
Q هي معيار Cochren الذي اقترحه V. Cohren في عام 1937. يتم استخدامه في الحالات التي تتعرض فيها مجموعات من المواد المتجانسة لأكثر من اثنين والتي يكون من الممكن إجابتها - سلبي مشروط (0) وإيجابي مشروط (1) . تتكون الفرضية الفارغة من تأثيرات متساوية للتأثير. يتيح تحليل التباين ثنائي الاتجاه تحديد وجود تأثيرات المعالجة ، لكن لا يتيح تحديد الأعمدة التي يوجد بها هذا التأثير. لحل هذه المشكلة ، يتم استخدام طريقة معادلات Sheffe متعددة للعينات المزدوجة.
تحليل متعدد المتغيرات
تنشأ مهمة التحليل متعدد المتغيرات عندما يكون من الضروري تحديد تأثير شرطين أو أكثر على متغير عشوائي معين. توفر الدراسة وجود متغير عشوائي واحد معتمد ، يتم قياسه على مقياس الاختلاف أو العلاقات ، والعديد من المتغيرات المستقلة ، يتم التعبير عن كل منها في مقياس الأسماء أو في الترتيب. تحليل بيانات التباين هو قسم مطور إلى حد ما من الإحصاءات الرياضية ، والذي يحتوي على الكثير من الخيارات. مفهوم البحث شائع لكل من عامل واحد ومتعدد العوامل. جوهرها هو أن التباين الكلي ينقسم إلى مكونات ، وهو ما يتوافق مع مجموعة معينة من البيانات. كل مجموعة بيانات لديها نموذج خاص بها.سننظر هنا فقط في الأحكام الأساسية الضرورية لفهم الخيارات الأكثر استخدامًا واستخدامها العملي.
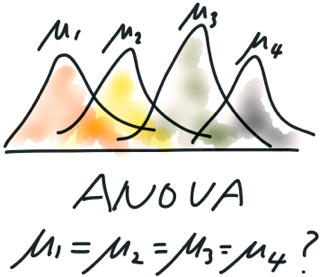
يتطلب تحليل تباين العوامل اتخاذ موقف دقيق إلى حد ما في جمع وعرض بيانات المدخلات ، وخاصة لتفسير النتائج. على عكس عامل واحد ، يمكن وضع نتائجه بشكل تعسفي في تسلسل معين ، تتطلب نتائج العاملين تمثيلًا أكثر تعقيدًا. ينشأ موقف أكثر صعوبة عندما يكون هناك ثلاثة أو أربعة أو أكثر من الظروف. وبسبب هذا ، نادراً ما يتم تضمين أكثر من ثلاثة (أربعة) شروط في نموذج. مثال على ذلك هو حدوث الرنين عند قيمة معينة من السعة ومحاثة الدائرة الكهربائية ؛ مظهر من التفاعل الكيميائي مع مجموعة معينة من العناصر التي تم بناء النظام منها ؛ حدوث آثار غير طبيعية في النظم المعقدة مع تزامن معين من الظروف. إن وجود التفاعل يمكن أن يغير بشكل جذري نموذج النظام ويؤدي في بعض الأحيان إلى إعادة التفكير في طبيعة الظواهر التي يتعامل معها المجرب.
تحليل متعدد المتغيرات للاختلاف مع التجارب المتكررة
غالبًا ما يتم تجميع بيانات القياس ليس بواسطة اثنين ، ولكن حسب عدد أكبر من العوامل. لذلك ، إذا أخذنا بعين الاعتبار تحليل تباين العمر التشغيلي لإطارات عجلات حافلة العربات مع مراعاة الظروف (الشركة المصنعة والطريق الذي يتم تشغيل الإطارات به) ، فيمكننا تمييز الموسم الذي يتم فيه تشغيل الإطارات (أي فصل الشتاء والصيف) كحالة منفصلة. نتيجة لذلك ، سيكون لدينا مهمة طريقة ثلاثة عوامل.
إذا كان هناك المزيد من الشروط ، فإن النهج هو نفسه كما هو الحال في تحليل عاملين. في جميع الحالات ، يحاولون تبسيط النموذج. لا تظهر ظاهرة تفاعل عاملين في كثير من الأحيان ، والتفاعل الثلاثي يحدث فقط في حالات استثنائية. وهي تشمل التفاعل الذي توجد به معلومات سابقة وأسباب وجيهة لأخذها في الاعتبار في النموذج. عملية عزل العوامل الفردية وأخذها في الاعتبار بسيطة نسبياً. لذلك ، غالبًا ما تكون هناك رغبة في إبراز المزيد من الظروف. هذا لا ينبغي أن يتم بعيدا. كلما زادت الظروف ، كلما أصبح النموذج أقل موثوقية وكلما زاد احتمال الخطأ. يصبح النموذج نفسه ، الذي يتضمن عددًا كبيرًا من المتغيرات المستقلة ، صعبًا بدرجة كافية لتفسيره وغير مريح للاستخدام العملي.
الفكرة العامة لتحليل التباين
تحليل التباين في الإحصاءات هو طريقة للحصول على نتائج الملاحظات التي تعتمد على مختلف الظروف الموجودة في وقت واحد ، وتقييم تأثيرها. يُطلق على المتغير المتحكم فيه والذي يتوافق مع طريقة التأثير على موضوع الدراسة وفي فترة زمنية معينة اكتسب قيمة معينة عاملًا. يمكن أن تكون النوعية والكمية. تكتسب مستويات الظروف الكمية قيمة معينة على مقياس رقمي. ومن الأمثلة على ذلك درجة الحرارة والضغط وكمية المادة. العوامل النوعية هي مواد مختلفة وأساليب تكنولوجية مختلفة وأجهزة وأجهزة مالئة. مستوياتها تتوافق مع حجم الأسماء.
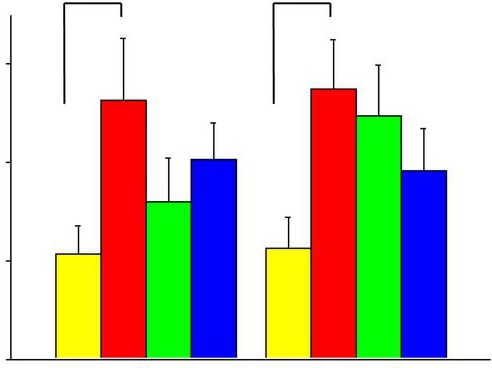
يمكن أن تشمل الجودة أيضا نوع من مواد التعبئة والتغليف ، وظروف التخزين من شكل جرعة. كما أنه من المنطقي أن نعزو درجة طحن المواد الخام ، والتكوين الكسري للحبيبات ذات الأهمية الكمية ، ولكن يصعب التحكم فيها إذا تم استخدام مقياس كمي. يعتمد عدد عوامل الجودة على نوع شكل الجرعة ، وكذلك الخصائص الفيزيائية والتكنولوجية للمواد الطبية. على سبيل المثال ، يمكن الحصول على أقراص من المواد البلورية عن طريق الضغط المباشر. في هذه الحالة ، يكفي اختيار مواد منزلقة ومواد تشحيم.
أمثلة على العوامل النوعية لأنواع مختلفة من أشكال الدواء
- الصبغات. تكوين المستخرج ، نوع المستخرج ، طريقة تحضير المواد الخام ، طريقة الإنتاج ، طريقة الترشيح.
- مقتطفات (سائلة ، سميكة ، جافة). تكوين المستخرج ، طريقة الاستخراج ، نوع التثبيت ، طريقة إزالة المادة المستخرجة والصابورة.
- أقراص. تكوين سواغ ، الحشو ، تفكك ، المجلدات ، زيوت التشحيم و glidants. وهناك طريقة لإنتاج أقراص ، نوع من معدات التجهيز. نوع القشرة ومكوناتها ، صانعي الأفلام ، الأصباغ ، الأصباغ ، الملدنات ، المذيبات.
- حلول الحقن. نوع المذيبات ، طريقة الترشيح ، طبيعة المثبتات والمواد الحافظة ، ظروف التعقيم ، طريقة ملء الأمبولات.
- التحاميل. تكوين قاعدة تحميلة ، طريقة لإنتاج التحاميل ، الحشو ، التغليف.
- مرهم. تكوين القاعدة ، والمكونات الهيكلية ، وطريقة إعداد مرهم ، ونوع المعدات ، والتغليف.
- كبسولات. نوع مادة الصدفة ، طريقة إنتاج الكبسولات ، نوع الملدنات ، المواد الحافظة ، الصبغة.
- المراهم. طريقة التحضير والتكوين ونوع المعدات ونوع المستحلب.
- تعليق. نوع المذيب ، نوع المثبت ، طريقة التشتت.
أمثلة للعوامل النوعية ومستوياتها المدروسة في عملية تصنيع الأقراص
- مسحوق الخبز. نشا البطاطس ، الطين الأبيض ، خليط من بيكربونات الصوديوم مع حامض الستريك ، كربونات المغنيسيوم الأساسية.
- حل الموثق. الماء ، عجينة النشا ، شراب السكر ، محلول السليلوز الميثيلي ، محلول السليلوز الميثيل هيدروكسي بروبيل ، محلول البولي فينيل بيروليدون ، محلول كحول البولي فينيل.
- مادة الانزلاق. الهباء الجوي ، النشا ، التلك.
- حشو. السكر ، الجلوكوز ، اللاكتوز ، كلوريد الصوديوم ، فوسفات الكالسيوم.
- زيوت التشحيم. حامض دهني ، جليكول البولي إيثيلين ، البارافين.
تحليل نماذج التباين في دراسة القدرة التنافسية للدولة
أحد أهم المعايير لتقييم حالة الدولة ، والتي تقيّم مستوى رفاهها وتنميتها الاجتماعية الاقتصادية ، هي القدرة التنافسية ، أي مجموعة من الخصائص الملازمة للاقتصاد الوطني والتي تحدد قدرة الدولة على التنافس مع الدول الأخرى. بعد تحديد مكان ودور الدولة في السوق العالمية ، يمكننا وضع استراتيجية واضحة لضمان الأمن الاقتصادي على الصعيد الدولي ، لأنه مفتاح العلاقات الإيجابية بين روسيا وجميع اللاعبين في السوق العالمية: المستثمرين والدائنين وحكومات الدول.
لمقارنة مستوى القدرة التنافسية للبلدان ، يتم تصنيف البلدان باستخدام مؤشرات معقدة ، والتي تشمل مؤشرات مرجحة مختلفة. أساس هذه المؤشرات هو العوامل الرئيسية التي تؤثر على الوضع الاقتصادي والسياسي ، إلخ. توفر مجموعة من النماذج لدراسة القدرة التنافسية للدولة استخدام طرق التحليل الإحصائي متعدد المتغيرات (على وجه الخصوص ، تحليل التباين (الإحصائيات) ، نمذجة الاقتصاد القياسي ، اتخاذ القرارات) وتشمل الخطوات الرئيسية التالية:
- تشكيل نظام للمؤشرات المؤشرات.
- تقييم وتوقع مؤشرات القدرة التنافسية للدولة.
- مقارنة بين مؤشرات مؤشرات القدرة التنافسية للدول.
الآن النظر في محتوى نماذج كل مرحلة من مراحل هذا المجمع.
في المرحلة الاولى بمساعدة أساليب دراسة الخبراء ، يتم تشكيل مجموعة مبررة من المؤشرات الاقتصادية - مؤشرات لتقييم القدرة التنافسية للدولة مع الأخذ في الاعتبار تفاصيل تطوره على أساس التصنيفات والبيانات الدولية من الإدارات الإحصائية التي تعكس حالة النظام ككل وعملياته.هناك ما يبرر اختيار هذه المؤشرات من خلال الحاجة إلى اختيار تلك المؤشرات التي تجعل من أقصى حد من وجهة نظر الممارسة العملية من الممكن تحديد مستوى الدولة وجاذبيتها الاستثمارية وإمكانات التوطين النسبي للتهديدات الحالية المحتملة والحياة الحقيقية.
المؤشرات الرئيسية لأنظمة التصنيف الدولية هي المؤشرات:
- التنافسية العالمية (IGC).
- الحرية الاقتصادية (IES).
- التنمية البشرية (HDI).
- تصورات الفساد (CPI).
- التهديدات الداخلية والخارجية.
- إمكانات التأثير الدولي (IPMV).
المرحلة الثانية وهو يوفر لتقييم وتوقع مؤشرات القدرة التنافسية للدولة وفقا للتصنيفات الدولية ل 139 دولة في العالم.
المرحلة الثالثة يوفر مقارنة لشروط القدرة التنافسية للدول باستخدام الأساليب تحليل الارتباط والانحدار.
باستخدام نتائج الدراسة ، من الممكن تحديد طبيعة العمليات ككل وعن طريق المكونات الفردية للقدرة التنافسية للدولة ؛ اختبار فرضية تأثير العوامل وعلاقتها مع المناسبة مستوى الأهمية.
إن تنفيذ مجموعة النماذج المقترحة لن يسمح فقط بتقييم الوضع الحالي لمستوى القدرة التنافسية وجاذبية الدول ، ولكن أيضًا لتحليل نقاط الضعف في الإدارة ، ومنع أخطاء القرارات غير الصحيحة ، ومنع حدوث أزمة في الدولة.



