في النمذجة الإحصائية ، تحليل الانحدار هو دراسة تستخدم لتقييم العلاقة بين المتغيرات. تتضمن هذه الطريقة الرياضية العديد من الطرق الأخرى لنمذجة وتحليل العديد من المتغيرات ، عندما يكون التركيز على العلاقة بين المتغير التابع ومتغير واحد أو أكثر. وبشكل أكثر تحديدًا ، يساعد تحليل الانحدار على فهم كيفية تغير القيمة النموذجية للمتغير التابع في حالة تغير أحد المتغيرات المستقلة ، بينما تظل المتغيرات المستقلة الأخرى ثابتة.

في جميع الحالات ، يكون التقدير المستهدف دالة للمتغيرات المستقلة ويسمى دالة الانحدار. في تحليل الانحدار ، من المهم أيضًا وصف التغير في المتغير التابع كدالة للانحدار ، والتي يمكن وصفها باستخدام توزيع الاحتمالات.
مهام تحليل الانحدار
تُستخدم طريقة البحث الإحصائي هذه على نطاق واسع للتنبؤ ، حيث يكون لاستخدامها ميزة كبيرة ، ولكن في بعض الأحيان قد يؤدي إلى أوهام أو علاقات خاطئة ، لذلك يوصى باستخدامها بعناية في هذه المشكلة ، لأن الارتباط لا يعني ، على سبيل المثال ، وجود علاقة سببية.
تم تطوير عدد كبير من الطرق لإجراء تحليل الانحدار ، مثل الانحدار الخطي والعادية المربعات الصغرى ، والتي هي حدودي. جوهرها هو أن يتم تحديد وظيفة الانحدار من حيث عدد محدد من المعلمات غير المعروفة التي يتم تقديرها من البيانات. يسمح الانحدار اللامعلمي لوظائفه بالوقوع في مجموعة معينة من الوظائف ، والتي يمكن أن تكون غير محدودة الأبعاد.
كأسلوب بحث إحصائي ، يعتمد تحليل الانحدار في الممارسة على شكل عملية توليد البيانات ومدى ارتباطها بنهج الانحدار. نظرًا لأن الشكل الحقيقي لعملية البيانات يولد ، كقاعدة عامة ، رقمًا غير معروف ، فإن تحليل الانحدار للبيانات غالبًا ما يعتمد إلى حد ما على الافتراضات حول هذه العملية. يتم التحقق من هذه الافتراضات في بعض الأحيان إذا كان هناك ما يكفي من البيانات المتاحة. غالبًا ما تكون نماذج الانحدار مفيدة حتى عند انتهاك الافتراضات بشكل معتدل ، على الرغم من أنها لا تستطيع العمل بأقصى قدر من الكفاءة.
بمعنى أضيق ، قد يرتبط الانحدار بشكل خاص بتقييم متغيرات الاستجابة المستمرة ، على عكس متغيرات الاستجابة المنفصلة المستخدمة في التصنيف. تسمى حالة متغير الإخراج المستمر أيضًا الانحدار المتري من أجل التمييز بينه وبين المشكلات ذات الصلة.
القصة
أقرب أشكال الانحدار هي طريقة المربعات الصغرى المعروفة. تم نشره من قبل Legendre في عام 1805 و Gauss في عام 1809. طبق Legendre و Gauss هذه الطريقة على مهمة تحديد مدارات الأجسام حول الشمس (من المذنبات بشكل رئيسي ، لكن الكواكب الصغيرة المكتشفة حديثًا لاحقًا). نشر غاوس تطورا آخر لنظرية المربعات الصغرى في عام 1821 ، بما في ذلك نسخة من نظرية غاوس ماركوف.

لقد صاغ فرانسيس غالتون مصطلح "الانحدار" في القرن التاسع عشر لوصف ظاهرة بيولوجية. خلاصة القول هي أن نمو المتحدرين من نمو الأجداد ، كقاعدة عامة ، يتراجع إلى المتوسط الطبيعي.بالنسبة لجالتون ، كان للانحدار هذا المعنى البيولوجي فقط ، ولكن في وقت لاحق واصل عمله أدني يول وكارل بيرسون ووصل بهما إلى سياق إحصائي أكثر عمومية. في عمل Yule و Pearson ، يعتبر التوزيع المشترك لمتغيرات الاستجابة والمتغيرات الإيضاحية غوسية. رفض فيشر هذا الافتراض في أعمال عامي 1922 و 1925. اقترح فيشر أن التوزيع الشرطي لمتغير الاستجابة هو غاوسي ، ولكن لا ينبغي أن يكون التوزيع المشترك. في هذا الصدد ، فإن افتراض فيشر أقرب إلى صياغة غاوس عام 1821. حتى عام 1970 ، استغرق الأمر أحيانًا ما يصل إلى 24 ساعة للحصول على نتيجة تحليل الانحدار.

لا تزال طرق تحليل الانحدار مجالًا للبحث النشط. في العقود الأخيرة ، تم تطوير أساليب جديدة من أجل الانحدار الموثوق. الانحدار الذي ينطوي على ردود مترابطة ؛ طرق الانحدار التي تستوعب أنواعًا مختلفة من البيانات المفقودة ؛ الانحدار اللامعلمي. طرق الانحدار بايزي. الانحدارات التي يتم فيها قياس متغيرات التوقع مع وجود خطأ ؛ الانحدارات مع أكثر تنبؤات من الملاحظات ، وكذلك الاستدلالات السببية مع الانحدار.
نماذج الانحدار
تشمل نماذج تحليل الانحدار المتغيرات التالية:
- معلمات غير معروفة ، تم تعيينها على أنها تجريبية ، والتي قد تكون عددًا أو ناقلًا.
- المتغيرات المستقلة ، X.
- المتغيرات التابعة ، Y.
في مجالات العلوم المختلفة حيث يتم تطبيق تحليل الانحدار ، يتم استخدام مصطلحات مختلفة بدلاً من المتغيرات المستقلة والمستقلة ، ولكن في جميع الحالات يرتبط نموذج الانحدار Y بالوظائف X و β.
عادة ما يستغرق التقريب النموذج E (Y | X) = F (X ، β). لإجراء تحليل الانحدار ، يجب تحديد نوع الوظيفة f. أقل شيوعًا ، يعتمد على معرفة العلاقة بين Y و X التي لا تعتمد على البيانات. إذا كانت هذه المعرفة غير متوفرة ، فسيتم اختيار نموذج مرن أو مناسب F.
المتغير المتغير Y
لنفترض الآن أن متجه المعلمات غير المعروفة β له طول k. لإجراء تحليل الانحدار ، يجب على المستخدم تقديم معلومات حول المتغير التابع Y:
- إذا كانت هناك نقاط بيانات N من النموذج (Y ، X) ، حيث N
- إذا تم ملاحظة N = K بالضبط ، وكانت الدالة F خطية ، فيمكن حل المعادلة Y = F (X ، β) تمامًا ، وليس تقريبًا. هذا يقلل من حل مجموعة من المعادلات N مع N- المجهول (عناصر β) ، والتي لديها حل فريد طالما أن X مستقلة خطيا. إذا كانت F غير خطية ، فقد لا يكون الحل موجودًا ، أو قد توجد العديد من الحلول.
- الأكثر شيوعًا هو الموقف الذي يتم فيه ملاحظة نقاط N> إلى البيانات. في هذه الحالة ، توجد معلومات كافية في البيانات لتقييم القيمة الفريدة لـ β التي تتوافق بشكل أفضل مع البيانات ، ويمكن اعتبار نموذج الانحدار ، عند تطبيقه على البيانات ، نظامًا مفرط التحديد في β.
في الحالة الأخيرة ، يوفر تحليل الانحدار أدوات من أجل:
- إيجاد حلول لمعلمات غير معروفة β ، على سبيل المثال ، سوف تقلل المسافة بين القيم المقاسة والقيم المتوقعة لـ Y.
- في ظل افتراضات إحصائية معينة ، يستخدم تحليل الانحدار المعلومات الزائدة لتوفير معلومات إحصائية حول المعلمات غير المعروفة values والقيم المتوقعة للمتغير التابع Y.
عدد ضروري من القياسات المستقلة
النظر في نموذج الانحدار الذي يحتوي على ثلاثة معلمات غير معروفة: β0, β1 و β2. افترض أن المجرب ينفذ 10 قياسات بنفس قيمة المتغير المستقل للمتجه X.في هذه الحالة ، لا يوفر تحليل الانحدار مجموعة فريدة من القيم. أفضل شيء يمكنك القيام به هو تقييم المتوسط والانحراف المعياري للمتغير التابع Y. عن طريق قياس قيمتي X مختلفتين بنفس الطريقة ، يمكنك الحصول على بيانات كافية للانحدار مع مجهولين ، ولكن ليس لثلاثة مجهولين أو أكثر.

إذا تم إجراء قياسات المجرب على ثلاث قيم مختلفة للمتغير المستقل للمتجه X ، فإن تحليل الانحدار سيوفر مجموعة فريدة من التقديرات لثلاثة معلمات غير معروفة في β.
في حالة الانحدار الخطي العام ، فإن المعادلة المذكورة أعلاه تعادل شرط المصفوفة XتيX هو عكسها.
الافتراضات الإحصائية
عندما يكون عدد القياسات N أكبر من عدد المعلمات غير المعروفة k وخطأ القياس εأنا، كقاعدة عامة ، يتم توزيع فائض المعلومات الموجودة في القياسات واستخدامها للتنبؤات الإحصائية المتعلقة بالمعلمات غير المعروفة. هذا الفائض من المعلومات يسمى درجة حرية الانحدار.
الافتراضات الأساسية
تشمل الافتراضات الكلاسيكية لتحليل الانحدار ما يلي:
- العينة ممثلة للتنبؤ بالاستنتاج.
- الخطأ هو متغير عشوائي مع متوسط قيمة الصفر ، وهو مشروط على المتغيرات التفسيرية.
- يتم قياس المتغيرات المستقلة دون خطأ.
- كمتغيرات مستقلة (تنبؤات) ، فهي مستقلة خطيًا ، أي أنه لا يمكن التعبير عن أي تنبؤ في شكل مجموعة خطية من المتغيرات الأخرى.
- الأخطاء غير مترابطة ، أي مصفوفة التغاير للأخطاء القطرية وكل عنصر غير صفري هو تباين الخطأ.
- تباين الخطأ ثابت وفقًا للملاحظات (homoskedasticity). إذا لم يكن الأمر كذلك ، يمكنك استخدام طريقة المربعات الصغرى الأقل أهمية أو طرق أخرى.
تمتلك هذه الشروط الكافية لتقدير المربعات الصغرى الخصائص المطلوبة ، على وجه الخصوص ، تعني هذه الافتراضات أن تقديرات المعلمة ستكون موضوعية ومتسقة وفعالة ، خاصةً عند أخذها في الاعتبار في فئة التقديرات الخطية. من المهم أن نلاحظ أن الأدلة نادراً ما تفي بالشروط. بمعنى ، يتم استخدام الطريقة حتى لو كانت الافتراضات غير صحيحة. يمكن أحيانًا استخدام مجموعة متنوعة من الافتراضات كمقياس لمدى فائدة هذا النموذج. يمكن تخفيف الكثير من هذه الافتراضات بطرق أكثر تقدمًا. تتضمن تقارير التحليل الإحصائي عادة تحليل الاختبارات بناءً على بيانات العينة ومنهجية الأداة المساعدة للطراز.
بالإضافة إلى ذلك ، تشير المتغيرات في بعض الحالات إلى القيم المقاسة في مواقع النقاط. قد تكون هناك اتجاهات مكانية وارتباط تلقائي مكاني في المتغيرات التي تنتهك الافتراضات الإحصائية. الانحدار الجغرافي المرجح هو الطريقة الوحيدة التي تتعامل مع هذه البيانات.
تحليل الانحدار الخطي
في الانحدار الخطي ، الميزة هي أن المتغير التابع ، وهو Yأناهو مزيج خطي من المعلمات. على سبيل المثال ، في الانحدار الخطي البسيط ، يتم استخدام متغير مستقل واحد ، x ، لنمذجة نقاط nأنا، واثنين من المعلمات ، β0 و β1.
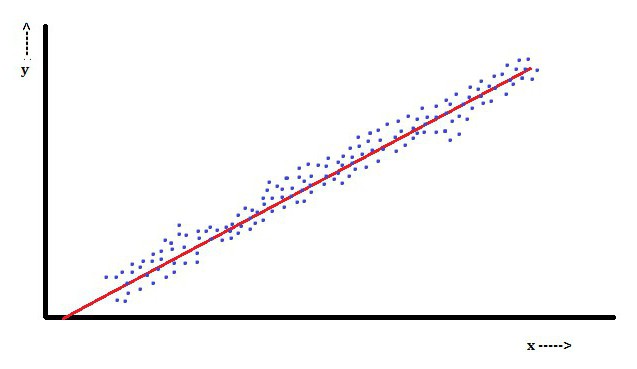
مع الانحدار الخطي المتعدد ، هناك العديد من المتغيرات المستقلة أو وظائفها.
مع أخذ عينات عشوائية من مجتمع ما ، فإن معالمه تجعل من الممكن الحصول على مثال لنموذج الانحدار الخطي.
في هذا الجانب ، تعد طريقة المربعات الصغرى هي الأكثر شعبية. باستخدامه ، يتم الحصول على تقديرات المعلمات التي تقلل من مجموع المخلفات التربيعية. يؤدي هذا النوع من التصغير (الذي يتميز بانحدار خطي) لهذه الوظيفة إلى مجموعة من المعادلات العادية ومجموعة من المعادلات الخطية ذات معلمات يتم حلها للحصول على تقديرات المعلمات.
في ظل افتراض إضافي بأن خطأ السكان ينتشر عادة ، يمكن للباحث استخدام هذه التقديرات للأخطاء القياسية لإنشاء فترات ثقة واختبار الفرضيات حول معالمها.
تحليل الانحدار غير الخطي
يشير المثال الذي لا تكون فيه الوظيفة خطية فيما يتعلق بالمعلمات إلى أنه يجب تقليل مجموع المربعات باستخدام إجراء تكراري. يقدم هذا العديد من المضاعفات التي تحدد الاختلافات بين أساليب المربعات الخطية وغير الخطية. وبالتالي ، فإن نتائج تحليل الانحدار باستخدام الطريقة غير الخطية تكون في بعض الأحيان غير متوقعة.
حساب القوة وحجم العينة
هنا ، كقاعدة عامة ، لا توجد طرق متسقة فيما يتعلق بعدد الملاحظات مقارنة بعدد المتغيرات المستقلة في النموذج. تم اقتراح القاعدة الأولى بواسطة Good and Hardin ويبدو أن N = t ^ n ، حيث N هو حجم العينة ، n هو عدد المتغيرات المستقلة ، و t هو عدد المشاهدات اللازمة لتحقيق الدقة المطلوبة إذا كان للنموذج متغير مستقل واحد فقط. على سبيل المثال ، يبني الباحث نموذج الانحدار الخطي باستخدام مجموعة بيانات تحتوي على 1000 مريض (N). إذا قرر الباحث أن هناك حاجة إلى خمس ملاحظات لتحديد الخط بدقة (م) ، فإن الحد الأقصى لعدد المتغيرات المستقلة التي يمكن أن يدعمها النموذج هو 4.
طرق أخرى
على الرغم من أن معلمات نموذج الانحدار عادةً ما يتم تقديرها باستخدام طريقة المربعات الصغرى ، إلا أن هناك طرقًا أخرى يتم استخدامها بشكل أقل كثيرًا. على سبيل المثال ، هذه هي الطرق التالية:
- طرق بايزي (مثل طريقة الانحدار الخطي بايزي).
- الانحدار في المئة ، وتستخدم في الحالات التي يعتبر فيها انخفاض في المئة من الأخطاء أكثر ملاءمة.
- أصغر انحرافات مطلقة ، والتي تكون أكثر ثباتًا في وجود القيم المتطرفة التي تؤدي إلى الانحدار الكمي.
- الانحدار اللامعلمي ، الذي يتطلب عددًا كبيرًا من الملاحظات والحسابات.
- مسافة مقياس التعلم ، والتي تتم دراستها بحثًا عن مسافة مترية كبيرة في مساحة إدخال معينة.
البرمجيات
يتم تنفيذ جميع حزم البرامج الإحصائية الرئيسية باستخدام تحليل الانحدار المربعات الصغرى. يمكن استخدام الانحدار الخطي البسيط وتحليل الانحدار المتعدد في بعض تطبيقات جداول البيانات ، وكذلك في بعض الآلات الحاسبة. على الرغم من أن العديد من حزم البرامج الإحصائية يمكن أن تؤدي أنواعًا مختلفة من الانحدار اللامعلمي والموثوق ، فإن هذه الطرق أقل توحيدًا ؛ حزم البرمجيات المختلفة تنفيذ أساليب مختلفة. تم تطوير برنامج الانحدار المتخصص للاستخدام في مجالات مثل تحليل الفحص والتصوير العصبي.






