يمثل مستوى الأهمية في الإحصاء مؤشرا هاما يعكس درجة الثقة في دقة وحقيقة البيانات المستلمة (المتوقعة). يستخدم هذا المفهوم على نطاق واسع في مجالات مختلفة: من إجراء البحوث الاجتماعية إلى الاختبارات الإحصائية للفرضيات العلمية.

تعريف
يُظهر مستوى الأهمية الإحصائية (أو النتيجة ذات الأهمية الإحصائية) ما هو احتمال حدوث مؤشرات عن طريق الخطأ. يتم التعبير عن الأهمية الإحصائية العامة للظاهرة بمعامل القيمة p (المستوى p). في أي تجربة أو ملاحظة ، من المحتمل أن تكون البيانات التي تم الحصول عليها ناتجة عن أخطاء في أخذ العينات. هذا صحيح خاصة بالنسبة لعلم الاجتماع.
بمعنى أن الإحصاء مهم إحصائيًا ، واحتمال حدوثه عرضي صغير للغاية أو يميل إلى التطرف. يعتبر المدقع في هذا السياق درجة انحراف الإحصائيات عن الفرضية الفارغة (فرضية يتم فحصها للتأكد من اتساقها مع بيانات العينة التي تم الحصول عليها). في الممارسة العلمية ، يتم اختيار مستوى الأهمية قبل جمع البيانات ، وكقاعدة عامة ، معاملها هو 0.05 (5 ٪). بالنسبة للأنظمة التي تكون فيها القيم الدقيقة مهمة للغاية ، يمكن أن يكون هذا المؤشر 0.01 (1٪) أو أقل.
تاريخ الحالة
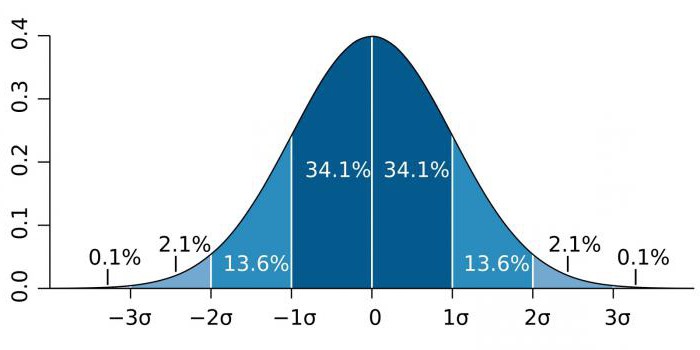
قدم عالم الإحصاء البريطاني وعالم الوراثة رونالد فيشر مفهوم مستوى الأهمية في عام 1925 عندما طور منهجية لاختبار الفرضيات الإحصائية. عند تحليل العملية ، هناك احتمال معين لظواهر معينة. تنشأ الصعوبات عند العمل مع احتمالات مئوية صغيرة (أو غير واضحة) والتي تندرج تحت مفهوم "خطأ القياس".
عند العمل مع إحصائيات غير محددة بما يكفي للتحقق ، واجه العلماء مشكلة الفرضية الخالية ، والتي "تتداخل" مع الكميات الصغيرة. اقترح فيشر تعريف هذه الأنظمة احتمال الأحداث 5٪ (0.05) كشريحة انتقائية ملائمة ، مما يسمح لك برفض الفرضية الفارغة في الحسابات.
إدخال معامل ثابت
في عام 1933 ، أوصى العلماء جيرزي نيومان وإيجون بيرسون في أعمالهما مقدمًا (قبل جمع البيانات) لتأسيس مستوى معين من الأهمية. أمثلة على استخدام هذه القواعد واضحة للعيان أثناء الانتخابات. لنفترض أن هناك مرشحين ، أحدهما شائع للغاية ، والثاني غير معروف. من الواضح أن المرشح الأول يفوز في الانتخابات ، وتميل فرص المرشح الثاني إلى الصفر. إنهم يكافحون - لكن ليسوا متساوين: هناك دائمًا احتمال القوة القاهرة والمعلومات المثيرة والقرارات غير المتوقعة التي يمكن أن تغير نتائج الانتخابات المتوقعة.
وافق نيومان وبيرسون على أن مستوى أهمية فيشر المقترح البالغ 0.05 (يرمز إليه بالرمز α) هو الأكثر ملاءمة. ومع ذلك ، فيشر نفسه في عام 1956 عارض تثبيت هذه القيمة. وأعرب عن اعتقاده أنه ينبغي تحديد مستوى α وفقا لظروف محددة. على سبيل المثال ، في فيزياء الجسيمات يكون 0.01.
مستوى أهمية P-
استخدم المصطلح p-value لأول مرة في أعمال Brownley's عام 1960. مستوى P (قيمة p) هو مؤشر مرتبط عكسيا بحقيقة النتائج. تقابل أعلى قيمة p p معامل أدنى مستوى من الثقة في عينة الاعتماد بين المتغيرات.
تعكس هذه القيمة احتمال حدوث أخطاء مرتبطة بتفسير النتائج. لنفترض أن مستوى p = 0.05 (1/20). يُظهر احتمال الخمسة بالمائة أن العلاقة بين المتغيرات الموجودة في العينة هي مجرد ميزة عشوائية للعينة.أي إذا كان هذا الاعتماد غائباً ، ثم مع مثل هذه التجارب المتكررة ، في المتوسط ، في كل دراسة العشرين ، يمكن للمرء أن يتوقع الاعتماد نفسه أو أكبر بين المتغيرات. في كثير من الأحيان ، يعتبر المستوى p "الهامش المقبول" لمستوى الخطأ.
بالمناسبة ، قد لا تعكس قيمة p العلاقة الحقيقية بين المتغيرات ، ولكنها تُظهر فقط متوسط قيمة معينة ضمن الافتراضات. على وجه الخصوص ، سيعتمد التحليل النهائي للبيانات أيضًا على القيم المحددة لهذا المعامل. مع مستوى p = 0.05 ، سيكون هناك بعض النتائج ، ومعامل 0.01 ، والبعض الآخر.
اختبار الفرضيات الإحصائية
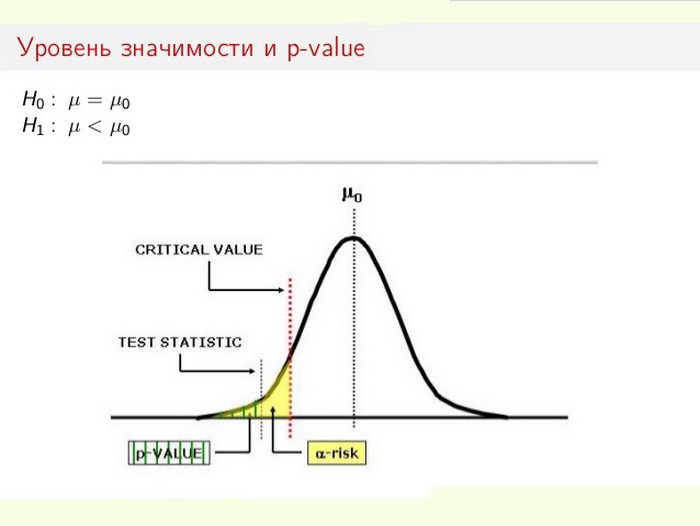
مستوى الأهمية الإحصائية مهم بشكل خاص عند اختبار الفرضيات. على سبيل المثال ، عند حساب اختبار ذي جانبين ، يتم تقسيم منطقة الرفض بالتساوي على طرفي توزيع العينة (بالنسبة إلى إحداثي الصفر) ويتم حساب حقيقة البيانات.
لنفترض ، عند مراقبة عملية معينة (ظاهرة) ، اتضح أن المعلومات الإحصائية الجديدة تشير إلى تغييرات صغيرة بالنسبة للقيم السابقة. علاوة على ذلك ، فإن التناقضات في النتائج صغيرة وليست واضحة ، ولكنها مهمة للدراسة. تنشأ المعضلة قبل الأخصائي: هل التغييرات تحدث بالفعل أم أن أخطاء أخذ العينات هذه (قياسات غير دقيقة)؟
في هذه الحالة ، يتم استخدام الفرضية الفارغة أو رفضها (كل ما يعزى إلى خطأ ما ، أو يتم التعرف على التغيير في النظام كأمر واقع). تعتمد عملية حل المشكلة على نسبة الدلالة الإحصائية الإجمالية (قيمة p) ومستوى الأهمية (α). إذا كان المستوى p <α ، فسيتم رفض فرضية فارغة. أصغر قيمة p ، والأهم من ذلك هو إحصاء الاختبار.
القيم المستخدمة
يعتمد مستوى الأهمية على المواد التي يتم تحليلها. في الممارسة العملية ، يتم استخدام القيم الثابتة التالية:
- α = 0.1 (أو 10٪) ؛
- α = 0.05 (أو 5٪) ؛
- α = 0.01 (أو 1٪) ؛
- α = 0.001 (أو 0.1٪).
كلما كانت الحسابات المطلوبة أكثر دقة ، انخفض معامل α. بطبيعة الحال ، تتطلب التنبؤات الإحصائية في الفيزياء والكيمياء والمستحضرات الصيدلانية وعلم الوراثة دقة أكبر مما كانت عليه في العلوم السياسية وعلم الاجتماع.

عتبات الأهمية في مجالات محددة
في المناطق عالية الدقة ، مثل فيزياء الجسيمات وأنشطة التصنيع ، غالبًا ما يتم التعبير عن الأهمية الإحصائية كنسبة الانحراف المعياري (المشار إليها بمعامل سيجما - relative) بالنسبة لتوزيع الاحتمالات العادي (توزيع غاوسي). statistical هو مؤشر إحصائي يحدد تشتت قيم ذات قيمة معينة بالنسبة للتوقعات الرياضية. تستخدم لرسم احتمالية الأحداث.
اعتمادًا على مجال المعرفة ، يختلف المعامل إلى حد كبير. على سبيل المثال ، عند التنبؤ بوجود بوزون هيغز ، المعلمة five هي 5 (σ = 5) ، والتي تتوافق مع القيمة p-value = 1 / 3.5 مليون ، في دراسات الجينوم ، يمكن أن يكون مستوى الأهمية 5 × 10-8ليست غير شائعة في هذا المجال.
فعالية
ضع في اعتبارك أن معاملات α والقيمة p ليست من الخصائص الدقيقة. مهما كان مستوى الأهمية في إحصائيات الظاهرة المدروسة ، فهو ليس أساسًا غير مشروط لقبول الفرضية. على سبيل المثال ، كلما كانت قيمة α أصغر ، زادت فرصة أن تكون الفرضية المحددة كبيرة. ومع ذلك ، هناك خطر الخطأ ، مما يقلل من القوة الإحصائية (أهمية) للدراسة.
قد يحصل الباحثون الذين يركزون فقط على النتائج المهمة إحصائياً على استنتاجات خاطئة. في الوقت نفسه ، من الصعب التحقق من عملهم ، حيث يستخدمون الافتراضات (التي هي في الواقع قيم α والقيمة p). لذلك ، يوصى دائمًا ، جنبًا إلى جنب مع حساب الأهمية الإحصائية ، بتحديد مؤشر آخر - حجم التأثير الإحصائي. حجم التأثير هو مقياس كمي لقوة التأثير.
