تحليل الانحدار الارتباط - هذه واحدة من أكثر الطرق شيوعًا لدراسة العلاقة بين القيم العددية. هدفها الرئيسي هو إيجاد العلاقة بين المعلمتين ودرجتها مع الاشتقاق التالي للمعادلة. على سبيل المثال ، لدينا طلاب اجتازوا اختبار الرياضيات واللغة الإنجليزية. يمكننا استخدام الارتباط لتحديد ما إذا كان نجاح اختبار ما يؤثر على النتائج في موضوع آخر. فيما يتعلق بتحليل الانحدار ، فإنه يساعد على التنبؤ بتقديرات الرياضيات بناءً على النقاط المسجلة في اختبار اللغة الإنجليزية ، والعكس بالعكس.

ما هو مخطط الارتباط؟
أي تحليل يبدأ بجمع المعلومات. كلما كان الأمر أكثر ، زادت دقة النتيجة التي تم الحصول عليها في النهاية. في المثال أعلاه ، لدينا اثنين من التخصصات التي يحتاج الطلاب إلى اجتياز الامتحان. معدل نجاحهم هو تقدير. يوضح تحليل الارتباط-الانحدار ما إذا كانت نتيجة موضوع واحد تؤثر على النقاط المسجلة في الامتحان الثاني. للإجابة على هذا السؤال ، من الضروري تحليل تصنيفات جميع الطلاب بالتوازي. ولكن عليك أولاً تحديد المتغير التابع. في هذه الحالة ، ليست مهمة للغاية. لنفترض أن امتحان الرياضيات قد تم في وقت سابق. النقاط عليه عبارة عن متغير مستقل (يتم تأجيلها على طول الحدود). اللغة الإنجليزية هي على الجدول الزمني في وقت لاحق. لذلك ، تعتمد التقديرات المستندة إليه على متغير تابع (يتم رسمه على طول الإحداثيات). كلما كان الرسم البياني الذي تم الحصول عليه بهذا الشكل يبدو كخط مستقيم ، كلما كان الارتباط الخطي أقوى بين القيمتين المحددتين. هذا يعني أن طلاب الرياضيات هم أكثر عرضة للاصطياد في اختبار اللغة الإنجليزية.
الافتراضات والتبسيط
تتضمن طريقة الارتباط وتحليل الانحدار إيجاد علاقة سببية. ومع ذلك ، في المرحلة الأولى ، يجب أن تفهم أن التغييرات في كلتا الكميتين يمكن أن تكون بسبب ثلث ما ، لم يأخذها الباحث في الاعتبار. يمكن أن يكون هناك أيضًا علاقات غير خطية بين المتغيرات ، وبالتالي ، فإن الحصول على معامل يساوي الصفر ليس نهاية التجربة.
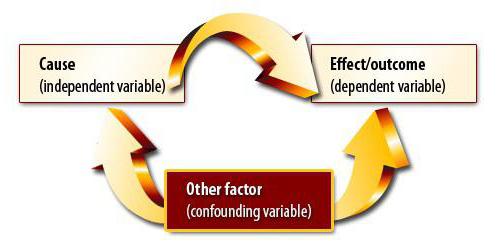
ارتباط بيرسون الخطي
يمكن استخدام هذا المعامل بشرط. الأول - جميع قيم المتغيرات هي أرقام عقلانية ، والثانية - من المتوقع أن تتغير القيم نسبيًا. يكون هذا المعامل دائمًا بين -1 و 1. إذا كان أكبر من الصفر ، فهناك اعتماد تناسبي مباشر ، أقل - على العكس ، متساوٍ - لا تؤثر هذه القيم على بعضها البعض بأي طريقة. القدرة على حساب هذا المؤشر هي أساس تحليل الارتباط والانحدار. لأول مرة ، تم تطوير هذا المعامل بواسطة كارل بيرسون بناءً على فكرة فرانسيس غالتون.
خصائص وتحذيرات
يعتبر معامل ارتباط بيرسون أداة قوية ، لكن يجب استخدامه بحذر أيضًا. التحذيرات التالية قيد الاستخدام:
- يشير معامل بيرسون إلى وجود أو عدم وجود علاقة خطية. لا ينتهي تحليل ارتباط الانحدار عند هذا الحد ، فقد يتضح أن المتغيرات مترابطة مع ذلك.
- يجب على المرء أن يكون حذرا في تفسير قيمة معامل. يمكن العثور على علاقة بين حجم الساق ومستوى الذكاء.ولكن هذا لا يعني أن أحد المؤشرات يحدد آخر.
- لا يقول معامل بيرسون أي شيء عن العلاقة السببية بين المؤشرات.

معامل ارتباط رتبة سبيرمان
إذا أدى أي تغيير في قيمة أحد المؤشرات إلى زيادة أو انخفاض في قيمة مؤشر آخر ، فإن هذا يعني أنها مرتبطة. يرتبط تحليل انحدار الارتباط ، والذي سيتم تقديم مثال على ذلك أدناه ، بدقة بمثل هذه المعلمات. يتيح لك معامل الرتبة تبسيط العمليات الحسابية.
تحليل الارتباط والانحدار: مثال
لنفترض أن هناك تقييمًا لفعالية عشر مؤسسات. لدينا قاضيان يعطيان النقاط. لا يمكن إجراء تحليل الارتباط والانحدار للمؤسسة في هذه الحالة على أساس معامل بيرسون الخطي. نحن لسنا مهتمين بالعلاقة بين تصنيفات القضاة. صفوف الشركات وفقا للقضاة مهمة.
هذا النوع من التحليل له المزايا التالية:
- شكل غير معلمي للعلاقات بين الكميات المدروسة.
- سهولة الاستخدام ، لأنه يمكن عزو الرتب بترتيب تصاعدي للقيمة وترتيب تنازلي.
الشرط الوحيد لهذا النوع من التحليل هو الحاجة إلى تحويل البيانات المصدر.
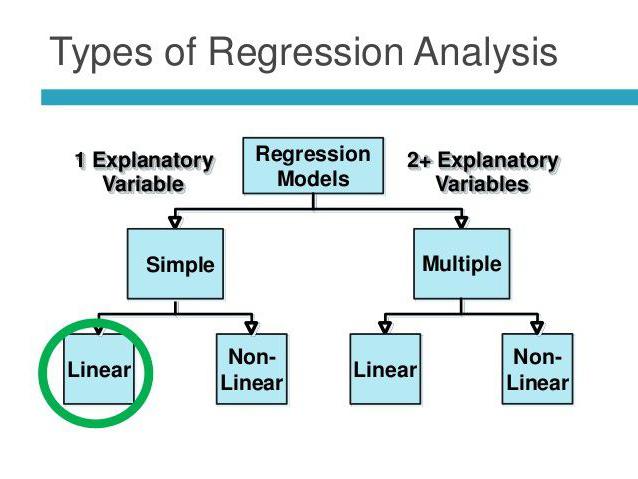
مشاكل التطبيق
يعتمد تحليل الارتباط والانحدار على الافتراضات التالية:
- تعتبر الملاحظات مستقلة (خسارة خمسة أضعاف من "النسر" لا تؤثر على نتيجة الوجه التالي للعملة).
- في تحليل الارتباط ، يعتبر كلا المتغيرين عشوائيًا. في الانحدار - واحد فقط (التابعة).
- عند اختبار الفرضيات ، يجب مراعاة التوزيع الطبيعي. يجب أن يكون التغيير في المتغير التابع هو نفسه بالنسبة لكل قيمة على الإحداث.
- إن مخطط الارتباط هو الاختبار الأول فقط للفرضية حول العلاقة بين سلسلتي المعلمات ، وليس النتيجة النهائية للتحليل.
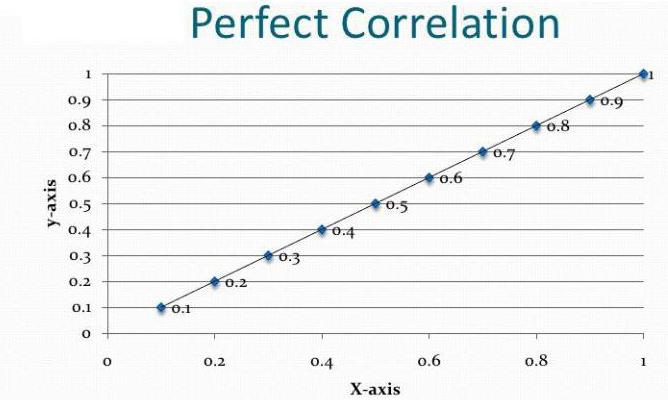
التبعية والسببية
لنفترض أننا قمنا بحساب معامل الارتباط لحجم الصادرات والناتج المحلي الإجمالي. اتضح أن يكون مساويا لموحدة الوحدة. هل قمنا بتحليل الارتباط والانحدار حتى النهاية؟ بالطبع لا. والنتيجة التي تم الحصول عليها لا تعني على الإطلاق أنه يمكن التعبير عن إجمالي الناتج المحلي من خلال التصدير. لم نثبت بعد وجود علاقة سببية بين المؤشرات. تحليل الانحدار الارتباط - التنبؤ قيم متغير واحد على أساس آخر. ومع ذلك ، تحتاج إلى فهم أنه غالبًا ما تؤثر العديد من العوامل على المعلمة. تحدد الصادرات إجمالي الناتج المحلي ، ولكن ليس فقط. هناك عوامل أخرى. يوجد هنا ارتباط ، وعلاقة سببية ، وإن كانت مضبوطة للمكونات الأخرى للناتج المحلي الإجمالي.
الوضع الآخر أكثر خطورة. في المملكة المتحدة ، تم إجراء مسح أظهر أن الأطفال الذين يدخن آباؤهم كانوا في كثير من الأحيان مجرمين. يستند هذا الاستنتاج إلى وجود علاقة قوية بين المؤشر. لكن هل هو صحيح؟ أولاً ، يمكن أن يكون الاعتماد معكوسًا. يمكن للوالدين البدء بالتدخين بسبب الضغط الناتج عن حقيقة أن أطفالهم يتورطون باستمرار في التعديلات ويخالفون القانون. ثانيا ، قد يكون كلا المعلمات بسبب الثالثة. هذه الأسر تنتمي إلى الطبقات الاجتماعية المنخفضة ، والتي تتميز كل المشاكل. لذلك ، بناءً على العلاقة المتبادلة ، لا يمكن الاستنتاج أن هناك علاقة سببية.
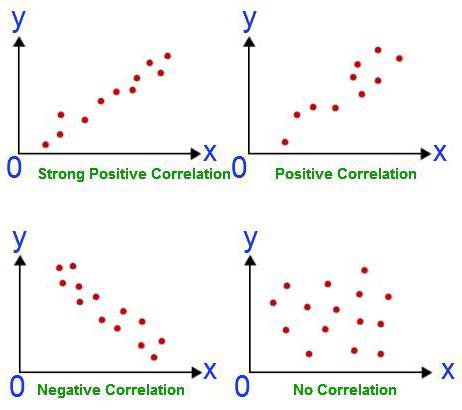
لماذا استخدام تحليل الانحدار؟
الاعتماد على الاعتماد ينطوي على إيجاد علاقات بين الكميات. العلاقة السببية في هذه الحالة لا تزال وراء الكواليس. تتطابق مهام الارتباط وتحليل الانحدار فقط من حيث تأكيد وجود علاقة بين قيمتين. ومع ذلك ، في البداية لا يهتم الباحث بإمكانية وجود علاقة سببية. يحتوي تحليل الانحدار دائمًا على متغيرين ، أحدهما يعتمد. يتم ذلك على عدة مراحل:
- اختيار النموذج الصحيح باستخدام طريقة المربعات الصغرى.
- اشتقاق معادلة تصف تأثير التغيير في متغير مستقل على آخر.
على سبيل المثال ، إذا قمنا بدراسة تأثير العمر على النمو البشري ، فإن تحليل الانحدار يمكن أن يساعد في التنبؤ بالتغيرات على مر السنين.
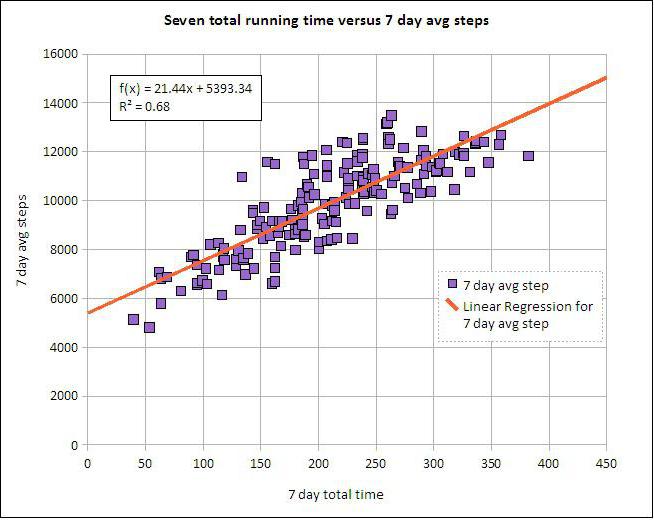
الانحدار الخطي والمتعدد
افترض أن X و Y هما متغيرين مرتبطين. يسمح لنا تحليل الانحدار بالتنبؤ بحجم أحدهم استنادًا إلى قيم الآخر. على سبيل المثال ، النضج والعمر من الأعراض التابعة. تنعكس العلاقة بينهما باستخدام الانحدار الخطي. في الواقع ، يمكنك التعبير عن X خلال Y أو العكس. لكن غالبًا ما يكون خط الانحدار صحيحًا. يعتمد نجاح التحليل إلى حد كبير على التحديد الصحيح للمتغير المستقل. على سبيل المثال ، لدينا مؤشران: العائد والهطول. من التجربة اليومية ، يصبح من الواضح أن الأول يعتمد على الثاني وليس العكس.
يسمح لك الانحدار المتعدد بحساب قيمة غير معروفة بناءً على قيم ثلاثة أو أكثر من المتغيرات. على سبيل المثال ، يعتمد إنتاج الأرز لكل فدان من الأرض على جودة الحبوب وخصوبة التربة والأسمدة ودرجة الحرارة وهطول الأمطار. كل هذه المعلمات تؤثر على النتيجة الإجمالية. لتبسيط النموذج ، يتم استخدام الافتراضات التالية:
- العلاقة بين الخصائص المستقلة والتأثيرية خطية.
- يتم استبعاد متعدد الخطوط. هذا يعني أن المتغيرات التابعة ليست مترابطة.
- الشذوذ الجنسي وعادية من سلسلة من الأرقام.
استخدام الارتباط وتحليل الانحدار
هناك ثلاث حالات رئيسية لاستخدام هذه الطريقة:
- اختبار العلاقات عارضة بين الكميات. في هذه الحالة ، يحدد الباحث قيم المتغير ويكتشف ما إذا كانت تؤثر على التغيير في المتغير التابع. على سبيل المثال ، يمكنك إعطاء الناس جرعات مختلفة من الكحول وقياس ضغط الدم لديهم. في هذه الحالة ، يعرف الباحث بالتأكيد أن الأول هو سبب الثاني ، وليس العكس. يتيح لك تحليل ارتباط الانحدار اكتشاف علاقة خطية متناسبة مباشرة بين هذين المتغيرين واستخلاص صيغة تصفه. في هذه الحالة ، يمكن مقارنة القيم المعبر عنها بوحدات قياس مختلفة تمامًا.
- العثور على علاقة بين اثنين من المتغيرات دون تمديد العلاقة السببية لهم. في هذه الحالة ، لا يوجد فرق بين حجم الباحث الذي يعتمد عليه. علاوة على ذلك ، في الواقع ، قد يتضح أن كليهما يتأثر بالمتغير الثالث ، وبالتالي يتغيران بشكل متناسب.
- حساب قيم كمية واحدة على أساس آخر. يعتمد على معادلة يتم استبدال الأرقام المعروفة بها.
وبالتالي ، يتضمن تحليل الارتباط إيجاد صلة (غير سببية) بين المتغيرات ، ويوضح تحليل الانحدار ، باستخدام دالة رياضية في الغالب.








