In statistische modellering is regressieanalyse een studie die wordt gebruikt om de relatie tussen variabelen te beoordelen. Deze wiskundige methode omvat vele andere methoden voor het modelleren en analyseren van verschillende variabelen, wanneer de nadruk ligt op de relatie tussen de afhankelijke variabele en een of meer onafhankelijke. Meer specifiek helpt regressieanalyse om te begrijpen hoe een typische waarde van een afhankelijke variabele verandert als een van de onafhankelijke variabelen verandert, terwijl de andere onafhankelijke variabelen vast blijven.

In alle gevallen is de doelschatting een functie van onafhankelijke variabelen en wordt deze de regressiefunctie genoemd. In regressieanalyse is het ook van belang om de verandering in de afhankelijke variabele te karakteriseren als een functie van regressie, die kan worden beschreven met behulp van een waarschijnlijkheidsverdeling.
Regressieanalyse-taken
Deze statistische onderzoeksmethode wordt veel gebruikt voor prognoses, waarbij het gebruik ervan een aanzienlijk voordeel heeft, maar soms kan het leiden tot illusies of valse relaties. Daarom wordt aanbevolen om het in deze kwestie zorgvuldig te gebruiken, omdat correlatie bijvoorbeeld geen causaal verband betekent.
Een groot aantal methoden is ontwikkeld voor het uitvoeren van regressieanalyse, zoals lineaire en gewone kleinste kwadratenregressie, die parametrisch zijn. Hun essentie is dat de regressiefunctie wordt gedefinieerd in termen van een eindig aantal onbekende parameters die worden geschat op basis van de gegevens. Niet-parametrische regressie maakt het mogelijk dat zijn functies in een bepaalde reeks functies liggen, die oneindig-dimensionaal kunnen zijn.
Als statistische onderzoeksmethode hangt de regressieanalyse in de praktijk af van de vorm van het gegevensgeneratieproces en hoe deze zich verhoudt tot de regressiebenadering. Aangezien de ware vorm van het gegevensproces in de regel een onbekend aantal genereert, hangt regressieanalyse van de gegevens vaak tot op zekere hoogte af van de veronderstellingen over dit proces. Deze veronderstellingen worden soms geverifieerd als er voldoende gegevens beschikbaar zijn. Regressiemodellen zijn vaak nuttig, zelfs wanneer aannames gematigd worden geschonden, hoewel ze niet met maximale efficiëntie kunnen werken.
In engere zin kan regressie specifiek betrekking hebben op de beoordeling van continue responsvariabelen, in tegenstelling tot de discrete responsvariabelen die in de classificatie worden gebruikt. Het geval van een continue uitvoervariabele wordt ook metrische regressie genoemd om deze te onderscheiden van gerelateerde problemen.
Het verhaal
De vroegste vorm van regressie is de bekende methode van de kleinste kwadraten. Het werd gepubliceerd door Legendre in 1805 en Gauss in 1809. Legendre en Gauss pasten de methode toe om uit astronomische waarnemingen de banen van lichamen rond de zon te bepalen (voornamelijk kometen, maar later pas ontdekte kleinere planeten). Gauss publiceerde een verdere ontwikkeling van de theorie van de kleinste kwadraten in 1821, inclusief een versie van de stelling van Gauss-Markov.

De term "regressie" werd bedacht door Francis Galton in de 19e eeuw om een biologisch fenomeen te beschrijven. Het komt erop neer dat de groei van afstammelingen van de groei van voorouders in de regel terugloopt naar het normale gemiddelde.Voor Galton had regressie alleen deze biologische betekenis, maar later werd zijn werk voortgezet door Udney Yule en Karl Pearson en in een meer algemene statistische context gebracht. In het werk van Yule en Pearson wordt de gezamenlijke verdeling van responsvariabelen en verklarende variabelen als Gauss beschouwd. Deze veronderstelling werd door Fisher verworpen in de werken van 1922 en 1925. Fisher suggereerde dat de voorwaardelijke verdeling van de responsvariabele Gaussiaans is, maar de gezamenlijke verdeling zou dat niet moeten zijn. In dit opzicht ligt de veronderstelling van Fischer dichter bij de Gauss-formulering van 1821. Tot 1970 duurde het soms tot 24 uur om het resultaat van een regressieanalyse te krijgen.

Methoden voor regressieanalyse blijven een gebied van actief onderzoek. In de afgelopen decennia zijn nieuwe methoden ontwikkeld voor betrouwbare regressie; regressie waarbij gecorreleerde reacties betrokken zijn; regressiemethoden voor verschillende soorten ontbrekende gegevens; niet-parametrische regressie; Bayesiaanse regressiemethoden; regressies waarin voorspellende variabelen met een fout worden gemeten; regressies met meer voorspellers dan waarnemingen, evenals causale gevolgtrekkingen met regressie.
Regressiemodellen
Regressieanalysemodellen omvatten de volgende variabelen:
- Onbekende parameters, aangeduid als bèta, die een scalair of vector kunnen zijn.
- Independent Variables, X.
- Afhankelijke variabelen, Y.
In verschillende wetenschapsgebieden waar regressieanalyse wordt toegepast, worden verschillende termen gebruikt in plaats van afhankelijke en onafhankelijke variabelen, maar in alle gevallen relateert het regressiemodel Y aan de functies X en β.
De benadering heeft meestal de vorm E (Y | X) = F (X, β). Om een regressieanalyse uit te voeren, moet het type functie f worden bepaald. Minder vaak is het gebaseerd op kennis van de relatie tussen Y en X die niet afhankelijk is van gegevens. Als dergelijke kennis niet beschikbaar is, wordt een flexibele of handige vorm F gekozen.
Afhankelijke variabele Y
Stel nu dat de vector van onbekende parameters β lengte k heeft. Om een regressieanalyse uit te voeren, moet de gebruiker informatie verstrekken over de afhankelijke variabele Y:
- Als er N-gegevenspunten van de vorm (Y, X) zijn, waarbij N
- Als precies N = K wordt waargenomen en de functie F lineair is, kan de vergelijking Y = F (X, β) exact worden opgelost, en niet ongeveer. Dit beperkt zich tot het oplossen van een reeks N-vergelijkingen met N-onbekenden (elementen van β), die een unieke oplossing heeft zolang X lineair onafhankelijk is. Als F niet-lineair is, bestaat de oplossing mogelijk niet of bestaan er veel oplossingen.
- De meest voorkomende is de situatie waarin N> naar de gegevens verwijst. In dit geval is er voldoende informatie in de gegevens om de unieke waarde voor β te evalueren die het beste overeenkomt met de gegevens, en het regressiemodel, wanneer toegepast op de gegevens, kan worden beschouwd als een overbepaald systeem in β.
In het laatste geval biedt regressieanalyse hulpmiddelen voor:
- Oplossingen vinden voor onbekende parameters β, die bijvoorbeeld de afstand tussen de gemeten en voorspelde waarden van Y minimaliseren.
- Onder bepaalde statistische veronderstellingen gebruikt regressieanalyse overtollige informatie om statistische informatie te verschaffen over onbekende parameters β en de voorspelde waarden van de afhankelijke variabele Y.
Noodzakelijk aantal onafhankelijke metingen
Overweeg een regressiemodel dat drie onbekende parameters heeft: β0, β1 en β2. Stel dat de experimentator 10 metingen uitvoert in dezelfde waarde van de onafhankelijke variabele van de vector X.In dit geval biedt regressieanalyse geen unieke set waarden. Het beste wat u kunt doen, is het gemiddelde en de standaarddeviatie van de afhankelijke variabele Y evalueren. Door twee verschillende X-waarden op dezelfde manier te meten, kunt u voldoende gegevens krijgen voor een regressie met twee onbekenden, maar niet voor drie of meer onbekenden.

Als de metingen van de experimentator werden uitgevoerd bij drie verschillende waarden van de onafhankelijke variabele van de vector X, levert de regressieanalyse een unieke set schattingen op voor drie onbekende parameters in β.
In het geval van algemene lineaire regressie, is de bovenstaande verklaring gelijk aan de eis dat de matrix XTX is omkeerbaar.
Statistische veronderstellingen
Wanneer het aantal metingen N groter is dan het aantal onbekende parameters k en de meetfout εikdan wordt in de regel het teveel aan informatie in de metingen vervolgens verdeeld en gebruikt voor statistische voorspellingen met betrekking tot onbekende parameters. Dit teveel aan informatie wordt de mate van regressievrijheid genoemd.
Fundamentele veronderstellingen
Klassieke veronderstellingen voor regressieanalyse zijn onder meer:
- De steekproef is representatief voor de voorspelling van inferenties.
- De fout is een willekeurige variabele met een gemiddelde waarde van nul, die afhankelijk is van de verklarende variabelen.
- Onafhankelijke variabelen worden zonder fouten gemeten.
- Als onafhankelijke variabelen (voorspellers) zijn ze lineair onafhankelijk, dat wil zeggen dat het niet mogelijk is om een voorspeller uit te drukken in de vorm van een lineaire combinatie van de andere.
- Fouten zijn niet gecorreleerd, d.w.z. de covariantiematrix van diagonale fouten en elk niet-nul element zijn de variantie van de fout.
- De variantie van de fout is constant volgens de waarnemingen (homoskedasticiteit). Als dit niet het geval is, kunt u de gewogen kleinste kwadratenmethode of andere methoden gebruiken.
Deze voldoende voorwaarden voor de schatting van de kleinste kwadraten hebben de vereiste eigenschappen, met name deze aannames betekenen dat de parameterschattingen objectief, consistent en effectief zullen zijn, vooral wanneer rekening wordt gehouden in de klasse van lineaire schattingen. Het is belangrijk op te merken dat bewijs zelden aan voorwaarden voldoet. Dat wil zeggen dat de methode wordt gebruikt, zelfs als de veronderstellingen niet waar zijn. Een variatie van veronderstellingen kan soms worden gebruikt als een maatstaf voor hoe nuttig dit model is. Veel van deze veronderstellingen kunnen worden beperkt door meer geavanceerde methoden. Statistische analyserapporten bevatten doorgaans een analyse van tests op basis van voorbeeldgegevens en methodologie voor het gebruik van modellen.
Bovendien verwijzen variabelen in sommige gevallen naar waarden gemeten op puntlocaties. Er kunnen ruimtelijke trends en ruimtelijke autocorrelatie zijn in variabelen die statistische veronderstellingen schenden. Geografische gewogen regressie is de enige methode die dergelijke gegevens verwerkt.
Lineaire regressieanalyse
Bij lineaire regressie is een kenmerk dat de afhankelijke variabele, die Y isikis een lineaire combinatie van parameters. In een eenvoudige lineaire regressie wordt bijvoorbeeld één onafhankelijke variabele, x, gebruikt om n-punten te modellereniken twee parameters, β0 en β1.
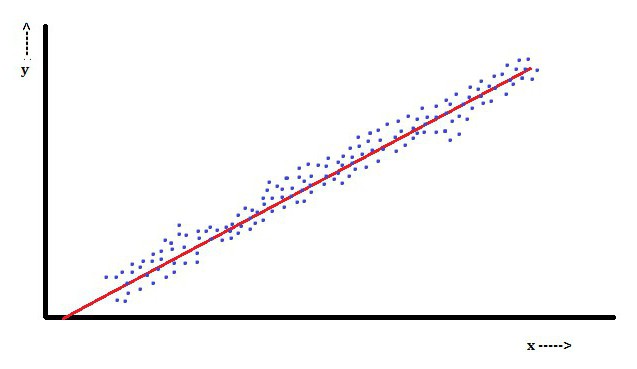
Met meervoudige lineaire regressie zijn er verschillende onafhankelijke variabelen of hun functies.
Met willekeurige steekproeven van een populatie, maken de parameters het mogelijk om een model van een lineair regressiemodel te verkrijgen.
In dit aspect is de methode met de kleinste kwadraten de meest populaire. Hiermee worden parameterschattingen verkregen die de som van de kwadratenresten minimaliseren. Dit soort minimalisatie (die kenmerkend is voor een lineaire regressie) van deze functie leidt tot een set normale vergelijkingen en een set lineaire vergelijkingen met parameters die worden opgelost om parameterschattingen te verkrijgen.
Onder de verdere veronderstelling dat de fout van de populatie zich meestal verspreidt, kan de onderzoeker deze schattingen van standaardfouten gebruiken om betrouwbaarheidsintervallen te creëren en hypothesen over zijn parameters te testen.
Niet-lineaire regressieanalyse
Een voorbeeld waarbij de functie niet lineair is ten opzichte van de parameters geeft aan dat de som van de vierkanten moet worden geminimaliseerd met behulp van een iteratieve procedure. Dit introduceert veel complicaties die de verschillen bepalen tussen lineaire en niet-lineaire kleinste kwadratenmethoden. Bijgevolg zijn de resultaten van regressieanalyse met behulp van de niet-lineaire methode soms onvoorspelbaar.
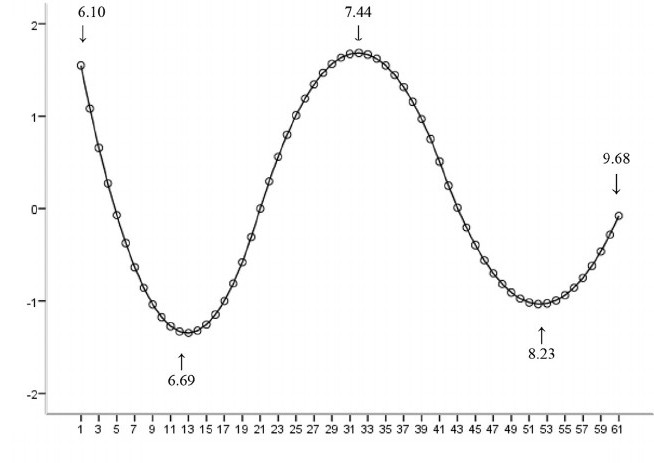
Berekening van vermogen en steekproefomvang
Hier zijn in de regel geen consistente methoden met betrekking tot het aantal waarnemingen vergeleken met het aantal onafhankelijke variabelen in het model. De eerste regel is voorgesteld door Good en Hardin en ziet eruit als N = t ^ n, waarbij N de steekproefgrootte is, n het aantal onafhankelijke variabelen is en t het aantal observaties dat nodig is om de gewenste nauwkeurigheid te bereiken als het model slechts één onafhankelijke variabele had. Een onderzoeker bouwt bijvoorbeeld een lineair regressiemodel met behulp van een gegevensset met 1000 patiënten (N). Als de onderzoeker besluit dat vijf observaties nodig zijn om de lijn (m) nauwkeurig te bepalen, dan is het maximale aantal onafhankelijke variabelen dat het model kan ondersteunen 4.
Andere methoden
Ondanks het feit dat de parameters van het regressiemodel meestal worden geschat met behulp van de kleinste kwadratenmethode, zijn er andere methoden die veel minder vaak worden gebruikt. Dit zijn bijvoorbeeld de volgende methoden:
- Bayesiaanse methoden (bijv. Bayesiaanse lineaire regressiemethode).
- Percentage regressie, gebruikt voor situaties waarin een vermindering van het percentage fouten meer geschikt wordt geacht.
- De kleinste absolute afwijkingen, die stabieler zijn in aanwezigheid van uitbijters die leiden tot kwantiele regressie.
- Niet-parametrische regressie, die een groot aantal observaties en berekeningen vereist.
- De afstand van de leermetriek, die wordt bestudeerd op zoek naar een significante metriekafstand in een bepaalde invoerruimte.
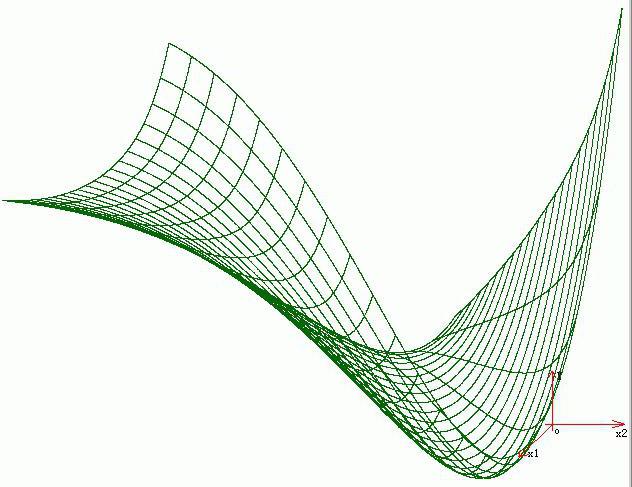
software
Alle belangrijke statistische softwarepakketten worden uitgevoerd met behulp van regressie-analyse met de kleinste kwadraten. Eenvoudige lineaire regressie en meervoudige regressieanalyse kunnen in sommige spreadsheettoepassingen worden gebruikt, evenals in sommige rekenmachines. Hoewel veel statistische softwarepakketten verschillende soorten niet-parametrische en betrouwbare regressie kunnen uitvoeren, zijn deze methoden minder gestandaardiseerd; verschillende softwarepakketten implementeren verschillende methoden. Gespecialiseerde regressiesoftware is ontwikkeld voor gebruik op gebieden zoals onderzoekanalyse en neuroimaging.






