Correlatieregressieanalyse - Dit is een van de meest gebruikelijke methoden om de relatie tussen numerieke waarden te bestuderen. Het belangrijkste doel is om de relatie tussen de twee parameters en de mate ervan te vinden met de daaropvolgende afleiding van de vergelijking. We hebben bijvoorbeeld studenten die geslaagd zijn voor het examen wiskunde en Engels. We kunnen correlatie gebruiken om te bepalen of het succes van een test de resultaten van een ander onderwerp beïnvloedt. Met betrekking tot regressie-analyse helpt het om wiskundige cijfers te voorspellen op basis van de gescoorde punten in een Engels examen en vice versa.

Wat is een correlatietabel?
Elke analyse begint met het verzamelen van informatie. Hoe meer het is, des te nauwkeuriger het uiteindelijk verkregen resultaat. In het bovenstaande voorbeeld hebben we twee disciplines waarin studenten moeten slagen voor een examen. Hun slagingspercentage is een schatting. Correlatie-regressie-analyse laat zien of het resultaat van één onderwerp de punten scoort die in het tweede examen zijn gescoord. Om deze vraag te beantwoorden, moeten de beoordelingen van alle studenten parallel worden geanalyseerd. Maar eerst moet u beslissen over de afhankelijke variabele. In dit geval is het niet zo belangrijk. Stel dat er eerder een wiskunde-examen heeft plaatsgevonden. Punten erop zijn een onafhankelijke variabele (ze worden uitgesteld langs de abscis). Engels staat later op het schema. Daarom zijn schattingen die hierop zijn gebaseerd een afhankelijke variabele (worden langs de ordinaat uitgezet). Hoe meer de aldus verkregen grafiek eruit ziet als een rechte lijn, hoe sterker de lineaire correlatie tussen de twee geselecteerde waarden. Dit betekent dat studenten wiskunde meer kans hebben om vijf op het Engelse examen te krijgen.
Veronderstellingen en vereenvoudigingen
De methode van correlatie- en regressieanalyse omvat het vinden van een oorzakelijk verband. In de eerste fase moet u echter begrijpen dat veranderingen in beide hoeveelheden het gevolg kunnen zijn van een derde, waarmee de onderzoeker nog geen rekening heeft gehouden. Er kunnen ook niet-lineaire relaties tussen de variabelen zijn, daarom is het verkrijgen van een coëfficiënt gelijk aan nul niet het einde van het experiment.
Pearson lineaire correlatie
Deze coëfficiënt kan worden gebruikt onder twee voorwaarden. De eerste - alle waarden van de variabelen zijn rationale getallen, de tweede - er wordt verwacht dat de waarden evenredig veranderen. Deze coëfficiënt is altijd tussen -1 en 1. Als deze groter is dan nul, dan is er een direct evenredige afhankelijkheid, minder - omgekeerd, gelijk - deze waarden beïnvloeden elkaar op geen enkele manier. Het vermogen om deze indicator te berekenen is de basis van correlatie- en regressieanalyse. Voor het eerst werd deze coëfficiënt ontwikkeld door Karl Pearson op basis van het idee van Francis Galton.
Eigenschappen en voorzorgsmaatregelen
Pearson's correlatiecoëfficiënt is een krachtig hulpmiddel, maar moet ook met voorzichtigheid worden gebruikt. De volgende waarschuwingen worden gebruikt:
- De Pearson-coëfficiënt geeft de aanwezigheid of afwezigheid van een lineaire relatie aan. Correlatie-regressieanalyse houdt daar niet op, het kan blijken dat de variabelen toch onderling verbonden zijn.
- Men moet voorzichtig zijn bij het interpreteren van de coëfficiëntwaarde. Er is een verband te vinden tussen beenlengte en IQ-niveau.Maar dit betekent niet dat de ene indicator de andere bepaalt.
- De Pearson-coëfficiënt zegt niets over het causale verband tussen de indicatoren.

Spearman's rang correlatiecoëfficiënt
Als een verandering in de waarde van de ene indicator leidt tot een toename of afname van de waarde van een andere, betekent dit dat ze gerelateerd zijn. Correlatie-regressieanalyse, waarvan hieronder een voorbeeld wordt gegeven, is precies verbonden met dergelijke parameters. Met rangcoëfficiënt kunt u de berekeningen vereenvoudigen.
Correlatie- en regressieanalyse: een voorbeeld
Stel dat er een beoordeling is van de effectiviteit van tien ondernemingen. We hebben twee rechters die hen punten geven. De correlatie- en regressieanalyse van de onderneming kan in dit geval niet worden uitgevoerd op basis van de lineaire Pearson-coëfficiënt. We zijn niet geïnteresseerd in de relatie tussen beoordelingen van juryleden. De rechters van de ondernemingen zijn volgens rechters belangrijk.
Dit type analyse heeft de volgende voordelen:
- Niet-parametrische vorm van relaties tussen de bestudeerde hoeveelheden.
- Gebruiksgemak, omdat de rangen zowel in oplopende volgorde van waarde als aflopende volgorde kunnen worden toegewezen.
De enige vereiste voor dit type analyse is de noodzaak om de brongegevens te converteren.
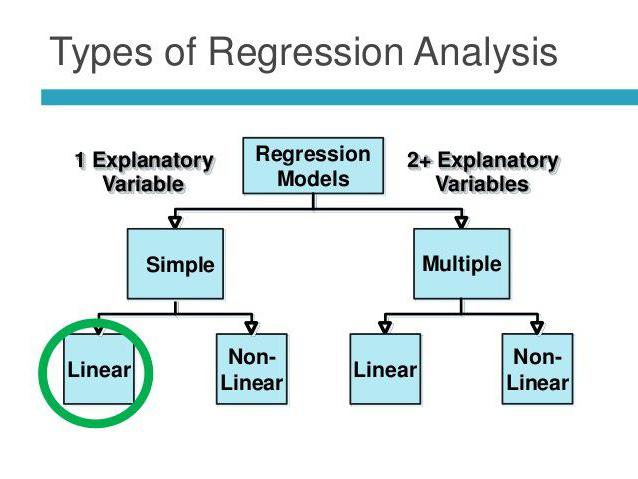
Applicatie problemen
De correlatie- en regressieanalyse is gebaseerd op de volgende veronderstellingen:
- Waarnemingen worden als onafhankelijk beschouwd (een vijfvoudig verlies van de "adelaar" heeft geen invloed op het resultaat van de volgende muntomdraai).
- In de correlatieanalyse worden beide variabelen als willekeurig beschouwd. In regressie - slechts één (afhankelijk).
- Bij het testen van een hypothese moet een normale verdeling in acht worden genomen. De verandering in de afhankelijke variabele moet hetzelfde zijn voor elke waarde op de abscis.
- Het correlatiediagram is slechts de eerste test van de hypothese over de relatie tussen de twee reeksen parameters, en niet het eindresultaat van de analyse.
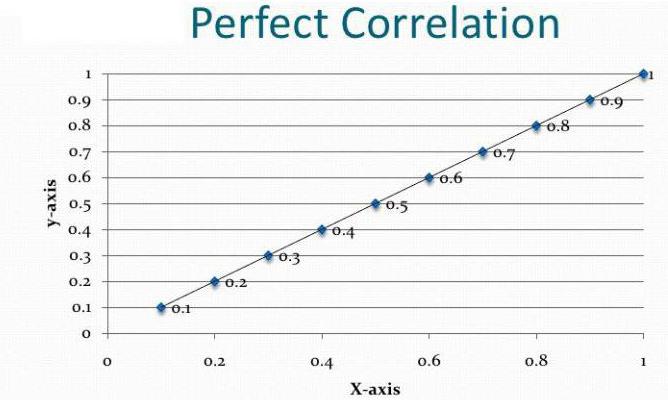
Afhankelijkheid en oorzakelijk verband
Stel dat we de correlatiecoëfficiënt van exportvolume en BBP hebben berekend. Het bleek gelijk te zijn aan modulo-eenheid. Hebben we correlatie- en regressieanalyses tot het einde uitgevoerd? Natuurlijk niet. Het verkregen resultaat betekent helemaal niet dat het BBP kan worden uitgedrukt door export. We hebben nog geen causaal verband tussen indicatoren aangetoond. Correlatie-regressieanalyse - voorspelling van de waarden van de ene variabele op basis van een andere. U moet echter begrijpen dat vaak veel factoren de parameter beïnvloeden. Export bepaalt het BBP, maar niet alleen het. Er zijn andere factoren. Hier is een verband en een oorzakelijk verband, zij het gecorrigeerd voor andere componenten van het bruto binnenlands product.
Een andere situatie is veel gevaarlijker. In het VK is een onderzoek uitgevoerd waaruit bleek dat kinderen van wie de ouders rookten vaker daders waren. Deze conclusie is gebaseerd op een sterke correlatie tussen de indicator. Maar heeft hij gelijk? Ten eerste kan de afhankelijkheid omgekeerd zijn. Ouders kunnen beginnen te roken vanwege stress vanwege het feit dat hun kinderen voortdurend in verandering raken en de wet overtreden. Ten tweede kunnen beide parameters te wijten zijn aan de derde. Dergelijke gezinnen behoren tot lage sociale klassen, die door beide problemen worden gekenmerkt. Daarom kan op basis van de correlatie niet worden geconcludeerd dat er een oorzakelijk verband is.
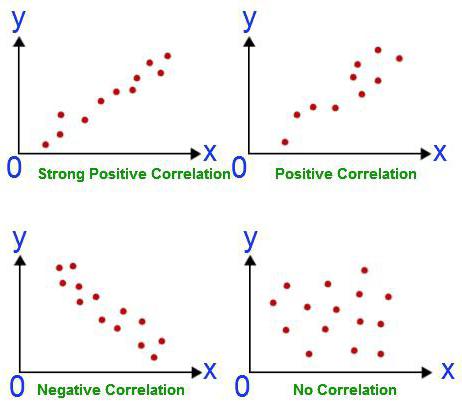
Waarom regressieanalyse gebruiken?
Correlatieafhankelijkheid omvat het vinden van relaties tussen hoeveelheden. Het causale verband blijft in dit geval achter de schermen. De taken van correlatie en regressieanalyse vallen alleen samen in termen van het bevestigen van het bestaan van een verband tussen de waarden van twee grootheden. Aanvankelijk let de onderzoeker echter niet op de mogelijkheid van een oorzakelijk verband. Regressieanalyse heeft altijd twee variabelen, waarvan er één afhankelijk is. Het vindt plaats in verschillende fasen:
- Het juiste model kiezen met de kleinste kwadratenmethode.
- Afleiding van een vergelijking die het effect beschrijft van een verandering in een onafhankelijke variabele op een andere.
Als we bijvoorbeeld het effect van leeftijd op de menselijke groei bestuderen, kan een regressieanalyse veranderingen in de loop van de jaren helpen voorspellen.
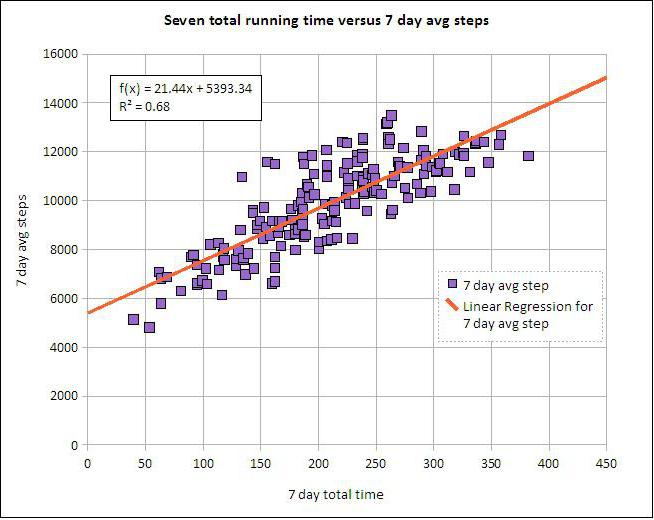
Lineaire en meervoudige regressie
Stel dat X en Y twee gerelateerde variabelen zijn. Regressie-analyse stelt ons in staat om de grootte van de ene te voorspellen op basis van de waarden van de andere. Volwassenheid en leeftijd zijn bijvoorbeeld afhankelijke symptomen. De relatie tussen hen wordt weerspiegeld met behulp van lineaire regressie. Je kunt X zelfs tot uitdrukking brengen via Y of omgekeerd. Maar vaak is slechts één van de regressielijnen correct. Het succes van de analyse hangt grotendeels af van de juiste bepaling van de onafhankelijke variabele. We hebben bijvoorbeeld twee indicatoren: opbrengst en neerslag. Uit de dagelijkse ervaring wordt duidelijk dat het eerste afhankelijk is van het tweede en niet andersom.
Met meervoudige regressie kunt u een onbekende waarde berekenen op basis van de waarden van drie of meer variabelen. De rijstopbrengst per hectare land is bijvoorbeeld afhankelijk van de graankwaliteit, bodemvruchtbaarheid, meststoffen, temperatuur en regenval. Al deze parameters beïnvloeden het algehele resultaat. Om het model te vereenvoudigen, worden de volgende veronderstellingen gebruikt:
- De relatie tussen onafhankelijke en beïnvloedende kenmerken is lineair.
- Multicollineariteit is uitgesloten. Dit betekent dat afhankelijke variabelen niet onderling verbonden zijn.
- Homoskedasticiteit en normaliteit van reeksen getallen.
Het gebruik van correlatie- en regressieanalyse
Er zijn drie belangrijke gevallen waarin deze methode wordt gebruikt:
- Toevallige relaties tussen hoeveelheden testen. In dit geval bepaalt de onderzoeker de waarden van de variabele en gaat hij na of deze de verandering in de afhankelijke variabele beïnvloeden. U kunt bijvoorbeeld mensen verschillende doses alcohol geven en hun bloeddruk meten. In dit geval weet de onderzoeker zeker dat de eerste de oorzaak is van de tweede en niet andersom. Correlatie-regressie-analyse stelt u in staat om een direct proportionele lineaire relatie tussen deze twee variabelen te detecteren en een formule af te leiden die deze beschrijft. In dit geval kunnen waarden uitgedrukt in volledig verschillende meeteenheden worden vergeleken.
- Een relatie vinden tussen twee variabelen zonder een causaal verband ermee uit te breiden. In dit geval is er geen verschil welke grootte de onderzoeker afhankelijk noemt. Bovendien kan het in werkelijkheid blijken dat ze allebei worden beïnvloed door de derde variabele en daarom veranderen ze evenredig.
- Berekening van de waarden van de ene hoeveelheid op basis van een andere. Het is gebaseerd op een vergelijking waarin bekende nummers worden vervangen.
Correlatieanalyse omvat dus het vinden van een verband (niet causaal) tussen variabelen, en regressieanalyse verklaart dit, vaak met behulp van een wiskundige functie.








