The compound word "extrapolation" is composed of two simple words. The first in Latin sounds extra and means "outside", "for", "outside". The second in the same Latin sounds polire and means "change", "straighten", "smooth". In general, extrapolation can be defined as a value outside two given points. It is considered an assessment of what is extracted from known facts that expand data in an unknown area to arrive at the intended result. This concept can also be attributed to the prediction of the image of the future, assuming the truth of present and past trends.
The extrapolation method assumes that data or observations in the future will continue to be similar. Thus, future results can be predicted. It can be considered as a mathematical hypothesis. Extrapolation uses the data and facts of a specific situation and provides predictions about what may happen in the end.
Extrapolation History

This method is often referred to as Richardson extrapolation or the Romberg method. But this is not entirely correct, since for centuries there have been similar numerical methods for solving such problems. Therefore, the famous Richardson h2 (extrapolation for a numerical solution) is not the first. A similar method was applicable in Huygens calculations as early as 1654. The term "extrapolation" itself was first coined by Thomas D. Clareson in 1959 in a book on science and fiction.
Extrapolation methods can be understood as the extension of data or processes, suggesting that a similar process will be applied outside of them. Extrapolation is an important concept used not only in mathematics, but also in other areas, such as sociology, psychology, forecasting. For example, a driver usually extrapolates driving conditions outside of his vision. Extrapolation can be attributed to a method in which data values are treated as points x1, x2 ..., xn, and then the value approaches the limit of a given range of points.
Benefits of use:
- A simple forecasting method.
- Not much data is required.
- Fast and cheap analytics.
The method exists in statistics. If any values are periodically removed, the answer approaches the next data point. An example of an extrapolation method is a weather forecast, which examines the background of the data and extrapolates the predicted model of the future. An even simpler example, if you have information about Sundays, Mondays and Tuesdays, you can extrapolate Wednesday or Thursday.
Disadvantages of using extrapolation:
- Unreliability, if there are significant fluctuations in historical data.
- The assumption that the past trend will continue in the future is hardly possible in many competitive business environments.
- Ignores quality factors, such as changes in tastes and fashion.
Sequence acceleration
Methods of extrapolation is to create a tangent line at the end of known data and expand it beyond this area. Like interpolation, extrapolation uses many methods that require prior knowledge of the process that creates the existing data points. The method includes linear and polynomial extrapolation, conics and French curve extrapolation.
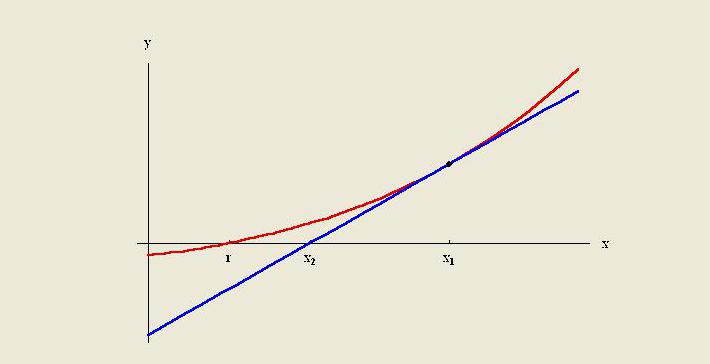
As a rule, the quality of a particular method is limited by assumptions about the function. In numerical analysis, Richardson extrapolation is a sequence acceleration method used to improve the rate of convergence.It is named after Lewis Fry Richardson. He introduced the calculation technique at the beginning of the 20th century, the usefulness of which for practical calculations can hardly be overestimated.
Practical applications of Richardson extrapolation include the Romberg integration, which applies it to the trapezoid rule and the Bulliers-Stoehr algorithm to solve ordinary differential equations.
Linear method
The linear extrapolation method is useful when a linear function is specified. This is done by drawing a tangent line at the end point of a given graph and expanding it beyond. This method of extrapolation in forecasting gives good results when the point to be predicted is not too far from the data. Linear interpolation is useful in finding values between given points. It can be considered as "filling in the gaps" of the data table.
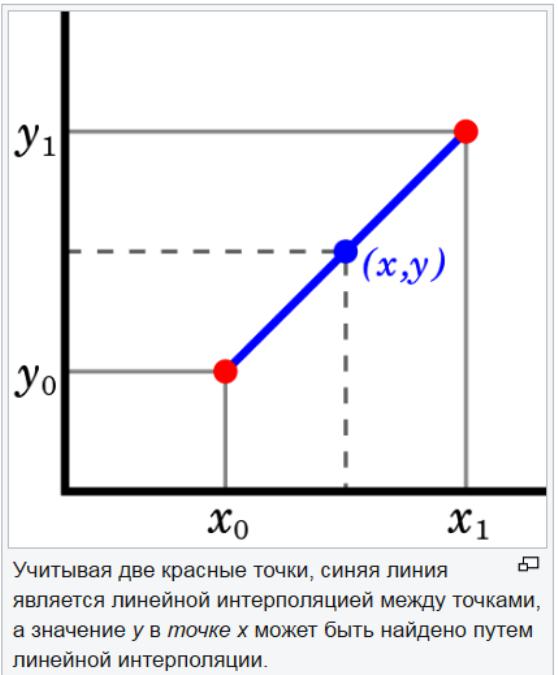
A linear interpolation strategy is to use a straight line to connect known points of values on either side of the unknown. Linear interpolation is not accurate for non-linear parameters. If the points in the data set change by a large amount, linear interpolation may give an incorrect estimate.
Linear extrapolation can help estimate values that are higher or lower than the values in the data set. Its strategy is to use a subset of data instead of the entire set. For this type of value, it is useful to apply the extrapolation method in forecasting using the last two or three points to estimate a value that exceeds the data range.
Polynomial and conical extrapolations
It is known that three points give a unique polynomial. A polynomial curve can be continued after the end of such data. It is usually carried out by the Newton method with a finite difference or using the Lagrange interpolation formula. A higher-order polynomial should be extrapolated with due care, because there is a fair chance of error with polynomial extrapolation. If this happens, the error estimate will increase exponentially with the degree of the polynomial.
In mathematics, minimal polynomial extrapolation is a sequence transformation used to accelerate convergence. Although Aitken's method is best known, it often fails, especially for vector sequences. In this case, an iteration is performed that constructs the matrix. Its columns are differences.

For example, an extrapolation method for a conical section can be made using 5 points indicated near the end of the data. In case the conical section is a circle or an ellipse, then it will loop back and reunite with itself. Parabola or hyperbola never intersect. But they can be bent back about the X axis. Extrapolation of the cone can be done on paper with a conical section or using a computer.
Mathematical Evaluation Method
In this extrapolation method, the value for the base period is predicted. The actions described below are automatically performed by the system and are not visible to the user. The description is intended to refine the algorithm, which displays the expected values from the amount stored in the system, and predicts the result of the meter measurement.
Extrapolation using the definition of the amount of the procedure is performed using the function: Yt = f (yi, t, aj).
As a basis for extrapolation, the rounded data of a typical base period stored in the reading results is added. The system determines the weight Yt of time series data in t (time of the forecast period) to obtain the correct solution by extrapolation. Where at the reference point are taken yi - the level of the series and aj - the parameter of the trend equation.
Feature Prediction
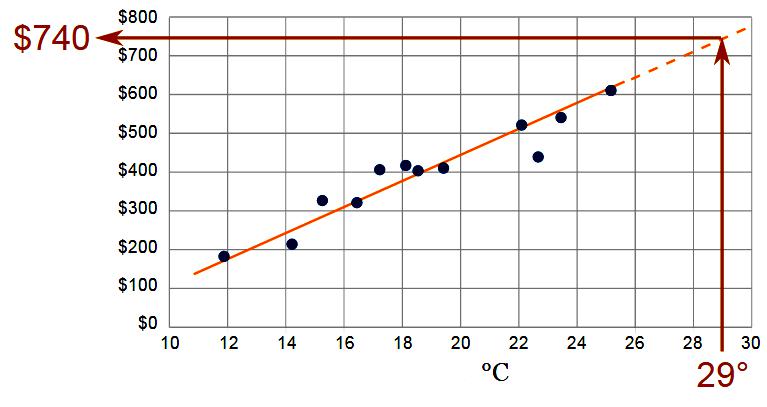
The method of fixing a statistical curve is applicable to predicting functionality.Statistical procedures correspond to the past data of one or more mathematical functions, such as linear, logarithmic, Fourier, or exponential. The best are selected by a statistical test. Then this forecast is extrapolated from this mathematical connection by the method of mathematical extrapolation. One of the easiest ways to get rough estimates of future (or past) conditions is to extrapolate data that changes over time.
For example, if you need to make a rough assessment of future levels of pollutants in drinking water for 20 years in advance, you can extrapolate this trend from the last 20 years. The same is observed if you need to estimate the prevalence of smoking or lung cancer in the background in the future. A forecast can be made by calculating trends over recent years. Extrapolations of this type can be done using less complex methods. In many cases (especially in the areas of marketing and business management), the extrapolation method is traditionally used, for example, by viewing the latest data and intuitively evaluating what is meant in the future.
Rule-based methods can also be used by applying a set of predefined principles or expectations based on a preliminary understanding of the system and taking into account the latest data to interpret future events.
With any extrapolation method, caution is important due to the presence of numerous uncertainties. Any extrapolation procedure is based on the assumption that reliable information is available in past data and knowledge. Consequently, the future is determined by the same factors that acted previously.
Forecasting Errors
The fallacy of extrapolation (more precisely, the fallacy of unjustified extrapolation) occurs when the phenomenon responsible for a number of trivial local effects is read as great global phenomena. Another reason for the error is that sometimes generalized rules are deduced from too few facts. Thus, Darwin’s theory of evolution is a fantastic example of the application of the extrapolation method, in which the mechanisms of random changes and natural selection are announced to take into account the development of such complex structures as the mammalian vision or the immune system of living organisms.
When attempting to interpret research results, the scientist should avoid extrapolation outside the data range and be aware of the underlying assumptions in order to avoid accepting invalid conclusions. In general, extrapolation is a legitimate scientific tool. There are two aspects that help distinguish between valid and erroneous extrapolation. The probability of erroneous extrapolation is higher when points for insufficient data were obtained for its construction.
Excel Statistical Tools
To find a correlation between years and results (for example, in a business), you can use Excel.
For these tasks, statistical tools for extrapolation modeling are used that are built into all versions of Excel, starting with 97. Procedure:
- Enter known values, for example, total sales for 2016-2017, if you need to determine them for 2018 and 2020.
- Install Analysis, a feature that requires the use of an add-in.
- To install it, extract from the menu "Tools", "Add-ons".
- Check the analysis utility window and confirm with “OK”.
- Measure correlations between two series.
- The extrapolation that needs to be done only makes sense if there is a clear trend (correlation) between the two sets of numbers (years and sales) by the method of extrapolating trends.
- To measure this correlation, use the menu "Tools", "Analysis Utilities".
- In the list “Analysis Tools” select “Correlation Analysis” and click “OK”.
- In the Input Range field enter the analyzed range, for example A6: B18, Excel will add the symbol "$".
- In the "Output Options" area, check the output range and enter it in the adjacent field.
- Confirm with OK.
- Excel creates an array of two rows in two columns. Find the calculated value (for example, 0.981). Since this value is close to 1, this means that there is a strong correlation between years and sales figures. If the user receives a value close to zero, this will mean that the trend does not occur. In this case, extrapolation does not make sense.
- An evaluation of future values starts.
- Select the required range and click the "Chart Wizard" button.
- Select a chart (for example, point clouds) and click Finish.
The use of moving averages
These two extrapolation methods involve the widespread use of sales data to predict the future. The moving average value takes a series of data and “smooths out” fluctuations in them. The goal is to extract extrema of data from period to period. Moving averages are often calculated quarterly or weekly. To predict future values, extrapolation involves the use of trends established by historical data. The main assumption of extrapolation is that the sample will continue in the future, unless actual evidence indicates otherwise. To understand these methods in more detail, you can consider a chart showing the sales of gadgets for large businesses from 2012 to 2015.
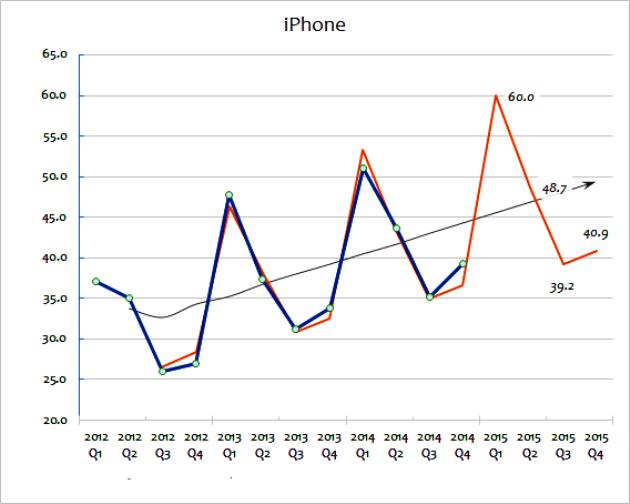
This calculation extrapolation method shows the actual sales figure. As you can see, the total amount of sales varies from year to year, although you can guess (looking at the data) that there is a general trend for sales growth. The black line shows the moving average. This is calculated by adding the last years of sales (e.g. Q1 + Q2 + Q3 + Q4) and then dividing by four.
This method smooths out annual changes and gives a good idea of the general trend in annual sales. A moving average helps to indicate a growth trend, expressed as a percentage. It is this extrapolation that will be used first to predict the path of future sales. This can be done mathematically using a spreadsheet. Alternatively, an extrapolated trend can simply be drawn on a chart as a rough estimate.
Trend correlation
Always one technology is the forerunner of another. This happens when the advances made in precursor technology can be adopted by follower technology. When such relationships exist, knowledge of changes in technology of predecessors can be used to predict the progress of technology followers in the future. In addition, extrapolation of the precursor allows predicting the continuation of the follow beyond the time delay.
In this case, the method of extrapolation of trends is used, in which, for example, the trends in the speed of military and transport aircraft are compared. Another example of trend correlation forecasting is predicting the size and power of future computers based on advances in microelectronic technology. Sometimes the technology of followers depends on several technologies of precursors, but not on one predecessor.
Fixed combinations of predecessors can affect the change in the sequence, but more often combinations are not fixed, and the inputs of the predecessors differ both in combination and in strength. For example, an increase in aircraft speed can occur due to the improvement of engines, materials, controls, fuel, aerodynamics and various combinations of these factors.
An example of a correlation forecast obtained by extrapolating trends: total passenger miles, total geographical miles, and average landing power.Extrapolation of statistically determined trends allows an objective approach to forecasting. However, this approach has serious limitations and pitfalls. Any errors or incorrect choices made in the determination of historical data will be reflected in the forecast, which reduces its value.
Applications, Attributes and Limits
The extrapolation method belongs to the field of forecasting. He suggests that patterns that existed in the past will continue into the future, and that these patterns are regular and can be measured. In other words, the past is a good indicator of the future. Applications are useful for developing baseline data.
Attributes and limits are simple and cheap calculation tools, as well as complex theoretical models.
- Process data - graphs and observations.
- The key is having a good database and understanding the structure within it.
- Technique is the best fit, ratio and so on.
Temporary standard statistical procedures do not lead to accurate selection of trends that the forecaster can extrapolate with comfort, performing the forecast by extrapolation. In such cases, the forecaster can “adjust” the statistical results using judgment. It can also completely ignore statistics and extrapolate the whole trend based on judgment.
Forecasts generated in this way are less accurate than statistical forecasts, but not necessarily unsatisfactory. One example of such an extrapolation of a quality trend is predicting aircraft complexity. Attempts to quantify this trend have not been successful. But the percentage of movable or adjustable parts of the aircraft was extrapolated with the frequency with which such elements were introduced in the past. These forecasts were fairly accurate.
Specific technical changes cannot be predicted in this way, but the degree of change can. This provides useful planning materials, indicating a trend in past behavior.
