Het significantieniveau in statistieken is een belangrijke indicator die de mate van vertrouwen in de nauwkeurigheid en waarheid van de ontvangen (voorspelde) gegevens weergeeft. Het concept wordt veel gebruikt op verschillende gebieden: van het uitvoeren van sociologisch onderzoek tot statistische toetsing van wetenschappelijke hypothesen.

definitie
Het niveau van statistische significantie (of statistisch significant resultaat) laat zien wat de waarschijnlijkheid is van een toevallig optreden van de bestudeerde indicatoren. De algemene statistische significantie van het fenomeen wordt uitgedrukt door de coëfficiënt p-waarde (p-niveau). In elk experiment of waarneming is het waarschijnlijk dat de verkregen gegevens te wijten zijn aan bemonsteringsfouten. Dit geldt vooral voor de sociologie.
Dat wil zeggen, een statistiek is statistisch significant, waarvan de kans op accidenteel optreden extreem klein is of extreem is. Extreem wordt in deze context beschouwd als de mate van afwijking van statistieken van de nulhypothese (een hypothese die wordt gecontroleerd op consistentie met de verkregen steekproefgegevens). In de wetenschappelijke praktijk wordt het significantieniveau gekozen vóór het verzamelen van gegevens en in de regel is de coëfficiënt 0,05 (5%). Voor systemen waar nauwkeurige waarden uiterst belangrijk zijn, kan deze indicator 0,01 (1%) of minder zijn.
anamnese
Het concept significantieniveau werd geïntroduceerd door de Britse statisticus en geneticus Ronald Fisher in 1925 toen hij een methode ontwikkelde voor het testen van statistische hypothesen. Bij het analyseren van een proces is er een zekere kans op bepaalde fenomenen. Moeilijkheden ontstaan bij het werken met kleine (of niet voor de hand liggende) procentkansen die vallen onder het concept 'meetfout'.
Bij het werken met statistieken die niet specifiek genoeg zijn om te verifiëren, werden wetenschappers geconfronteerd met het probleem van de nulhypothese, die "interfereert" met kleine hoeveelheden. Fisher stelde voor om voor dergelijke systemen te definiëren waarschijnlijkheid van gebeurtenissen 5% (0,05) als een handige selectieve schijf, waarmee u de nulhypothese in de berekeningen kunt verwerpen.
De introductie van een vaste coëfficiënt
In 1933 raden wetenschappers Jerzy Neumann en Egon Pearson in hun werk van tevoren aan (vóór gegevensverzameling) om een bepaald niveau van betekenis vast te stellen. Voorbeelden van het gebruik van deze regels zijn duidelijk zichtbaar tijdens de verkiezingen. Stel dat er twee kandidaten zijn, waarvan er één erg populair is en de tweede weinig bekend is. Het is duidelijk dat de eerste kandidaat de verkiezing wint en de kansen van de tweede neigen naar nul. Ze streven ernaar - maar niet gelijk: er is altijd de kans op overmacht, sensationele informatie, onverwachte beslissingen die de voorspelde verkiezingsresultaten kunnen veranderen.
Neumann en Pearson waren het erover eens dat Fisher's voorgestelde significantieniveau van 0,05 (aangeduid met het symbool α) het handigst is. Fisher zelf verzette zich echter in 1956 tegen de fixatie van deze waarde. Hij geloofde dat het niveau van α moet worden vastgesteld in overeenstemming met specifieke omstandigheden. In de deeltjesfysica is dit bijvoorbeeld 0,01.
Significantie niveau van p-
De term p-waarde werd voor het eerst gebruikt in het werk van Brownley in 1960. P-niveau (p-waarde) is een indicator die omgekeerd evenredig is aan de waarheid van de resultaten. De hoogste p-waarde komt overeen met het laagste betrouwbaarheidsniveau in de steekproef van afhankelijkheid tussen de variabelen.
Deze waarde geeft de kans op fouten weer die verband houden met de interpretatie van de resultaten. Stel dat p-niveau = 0,05 (1/20). Het toont de waarschijnlijkheid van vijf procent dat de relatie tussen de variabelen in de steekproef slechts een willekeurig kenmerk van de steekproef is.Dat wil zeggen, als deze afhankelijkheid afwezig is, kan men bij herhaalde dergelijke experimenten gemiddeld in elke twintigste studie dezelfde of grotere afhankelijkheid tussen de variabelen verwachten. Vaak wordt het p-niveau beschouwd als de "acceptabele marge" van het foutniveau.
Trouwens, p-waarde weerspiegelt misschien niet de werkelijke relatie tussen de variabelen, maar toont alleen een bepaalde gemiddelde waarde binnen de veronderstellingen. In het bijzonder zal de uiteindelijke analyse van de gegevens ook afhangen van de geselecteerde waarden van deze coëfficiënt. Met een p-niveau = 0,05 zullen er enkele resultaten zijn en met een coëfficiënt van 0,01 andere.
Statistische hypothesen testen
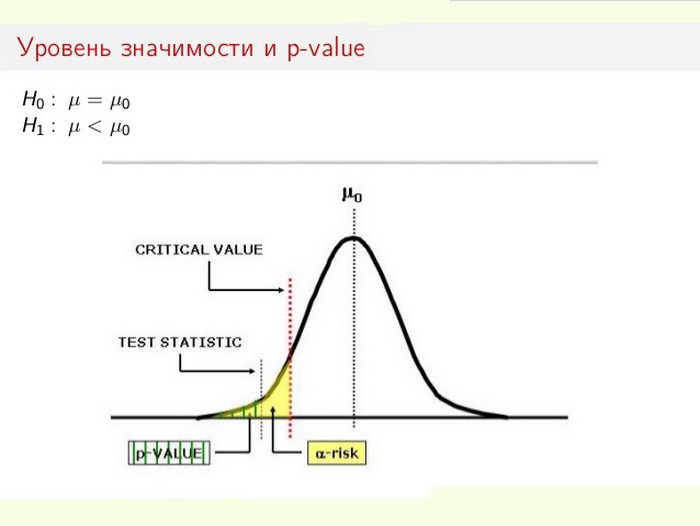
Het niveau van statistische significantie is vooral belangrijk bij het testen van hypothesen. Wanneer u bijvoorbeeld een tweezijdige test berekent, wordt het afwijzingsgebied gelijk verdeeld aan beide uiteinden van de steekproefverdeling (ten opzichte van de nulcoördinaat) en wordt de waarheid van de gegevens berekend.
Stel dat bij het monitoren van een bepaald proces (fenomeen) de nieuwe statistische informatie kleine veranderingen ten opzichte van eerdere waarden aangeeft. Bovendien zijn de discrepanties in de resultaten klein, niet voor de hand liggend, maar belangrijk voor het onderzoek. Het dilemma doet zich voor bij de specialist: vinden de veranderingen echt plaats of zijn deze bemonsteringsfouten (onnauwkeurige metingen)?
In dit geval wordt de nulhypothese gebruikt of afgewezen (alles wordt toegeschreven aan een fout of de verandering in het systeem wordt herkend als een voldongen feit). Het proces van het oplossen van het probleem is gebaseerd op de verhouding van totale statistische significantie (p-waarde) en significantieniveau (α). Als het p-niveau <α, wordt de nulhypothese verworpen. Hoe kleiner de p-waarde, des te belangrijker is de teststatistiek.
Gebruikte waarden
De mate van significantie hangt af van het materiaal dat wordt geanalyseerd. In de praktijk worden de volgende vaste waarden gebruikt:
- a = 0,1 (of 10%);
- a = 0,05 (of 5%);
- a = 0,01 (of 1%);
- a = 0,001 (of 0,1%).
Hoe nauwkeuriger de berekeningen nodig zijn, hoe lager de coëfficiënt α wordt gebruikt. Natuurlijk vereisen statistische voorspellingen in de natuurkunde, scheikunde, farmacie en genetica een grotere nauwkeurigheid dan in de politieke wetenschappen, sociologie.

Drempelwaarden voor specifieke gebieden
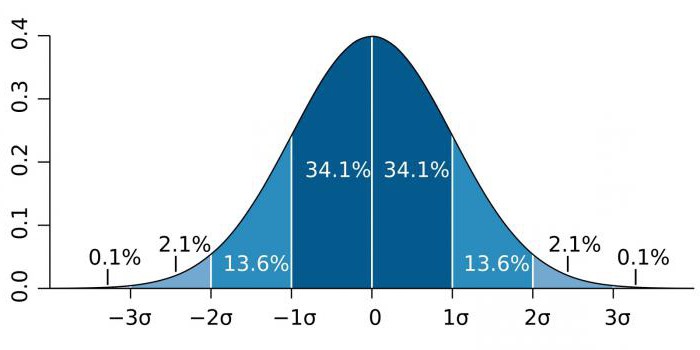
In gebieden met hoge precisie, zoals deeltjesfysica en productieactiviteiten, wordt statistische significantie vaak uitgedrukt als de verhouding van de standaardafwijking (aangegeven door de sigma-coëfficiënt - σ) ten opzichte van de normale waarschijnlijkheidsverdeling (Gauss-verdeling). σ is een statistische indicator die de spreiding van waarden van een bepaalde waarde ten opzichte van wiskundige verwachtingen bepaalt. Wordt gebruikt om de waarschijnlijkheid van gebeurtenissen te plotten.
Afhankelijk van het kennisveld varieert de coëfficiënt σ sterk. Wanneer bijvoorbeeld het bestaan van het Higgs-boson wordt voorspeld, is de parameter σ vijf (σ = 5), wat overeenkomt met de waarde p-waarde = 1 / 3,5 miljoen. In onderzoeken naar genomen kan het significantieniveau 5 × 10 zijn-8die niet ongewoon zijn voor dit gebied.
effectiviteit
Houd er rekening mee dat de coëfficiënten α en p-waarde geen nauwkeurige kenmerken zijn. Ongeacht het significantieniveau in de statistieken van het bestudeerde fenomeen, het is geen onvoorwaardelijke basis voor het accepteren van de hypothese. Hoe kleiner bijvoorbeeld de waarde van α, hoe groter de kans dat de vastgestelde hypothese significant is. Er is echter een risico op fouten, wat de statistische kracht (significantie) van het onderzoek vermindert.
Onderzoekers die zich uitsluitend op statistisch significante resultaten concentreren, kunnen verkeerde conclusies trekken. Tegelijkertijd is het moeilijk om hun werk dubbel te controleren, omdat ze aannames gebruiken (die in feite de waarden van α en p-waarde zijn). Daarom wordt het altijd aanbevolen om, samen met de berekening van de statistische significantie, een andere indicator te bepalen - de grootte van het statistische effect. De grootte van een effect is een kwantitatieve maat voor de sterkte van een effect.
