La esencia y los métodos de extrapolación.

La palabra compuesta "extrapolación" se compone de dos palabras simples. El primero en latín suena extra y significa "afuera", "para", "afuera". El segundo en el mismo latín suena polire y significa "cambio", "enderezar", "suave". En general, la extrapolación se puede definir como un valor fuera de dos puntos dados. Se considera una evaluación de lo que se extrae de hechos conocidos que expanden los datos en un área desconocida para llegar al resultado deseado. Este concepto también puede atribuirse a la predicción de la imagen del futuro, asumiendo la verdad de las tendencias presentes y pasadas.

El método de extrapolación supone que los datos u observaciones en el futuro continuarán siendo similares. Por lo tanto, se pueden predecir resultados futuros. Se puede considerar como una hipótesis matemática. La extrapolación utiliza los datos y hechos de una situación específica y proporciona predicciones sobre lo que puede suceder al final.

Historia de extrapolación

Este método a menudo se denomina extrapolación de Richardson o el método de Romberg. Pero esto no es del todo correcto, ya que durante siglos ha habido métodos numéricos similares para resolver tales problemas. Por lo tanto, el famoso Richardson h2 (extrapolación para una solución numérica) no es el primero. Un método similar era aplicable en los cálculos de Huygens ya en 1654. El término "extrapolación" fue acuñado por primera vez por Thomas D. Clareson en 1959 en un libro sobre ciencia y ficción.

Los métodos de extrapolación pueden entenderse como la extensión de datos o procesos, lo que sugiere que se aplicará un proceso similar fuera de ellos. La extrapolación es un concepto importante utilizado no solo en matemáticas, sino también en otras áreas, como la sociología, la psicología y el pronóstico. Por ejemplo, un conductor generalmente extrapola las condiciones de manejo fuera de su visión. La extrapolación se puede atribuir a un método en el que los valores de datos se tratan como puntos x1, x2 ..., xn, y luego el valor se acerca al límite de un rango de puntos dado.

Beneficios de uso:

1. Un método de pronóstico simple.
2. No se requieren muchos datos.
3. Análisis rápido y económico.

El método existe en las estadísticas. Si algún valor se elimina periódicamente, la respuesta se acerca al siguiente punto de datos. Un ejemplo de un método de extrapolación es un pronóstico del tiempo, que examina el fondo de los datos y extrapola el modelo predicho del futuro. Un ejemplo aún más simple, si tiene información sobre domingos, lunes y martes, puede extrapolar miércoles o jueves.

Desventajas de usar extrapolación:

1. Falta de fiabilidad, si hay fluctuaciones significativas en los datos históricos.
2. La suposición de que la tendencia pasada continuará en el futuro es casi imposible en muchos entornos comerciales competitivos.
3. Ignora los factores de calidad, como los cambios en los gustos y la moda.

Aceleración de secuencia

Los métodos de extrapolación son crear una línea tangente al final de los datos conocidos y expandirla más allá de esta área. Al igual que la interpolación, la extrapolación utiliza muchos métodos que requieren un conocimiento previo del proceso que crea los puntos de datos existentes. El método incluye extrapolación lineal y polinómica, cónicas y extrapolación de curva francesa.

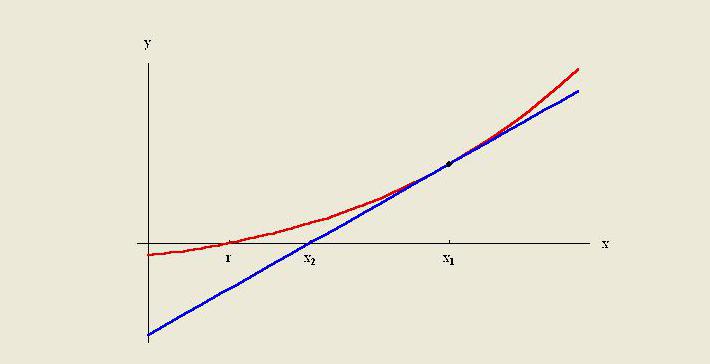
Como regla general, la calidad de un método particular está limitada por suposiciones sobre la función. En el análisis numérico, la extrapolación de Richardson es un método de aceleración de secuencia utilizado para mejorar la tasa de convergencia.Lleva el nombre de Lewis Fry Richardson. Introdujo la técnica de cálculo a principios del siglo XX, cuya utilidad para cálculos prácticos difícilmente se puede sobreestimar.

Las aplicaciones prácticas de la extrapolación de Richardson incluyen la integración de Romberg, que la aplica a la regla trapezoidal y al algoritmo de Bulliers-Stoehr para resolver ecuaciones diferenciales ordinarias.

Método lineal

El método de extrapolación lineal es útil cuando se especifica una función lineal. Esto se hace dibujando una línea tangente en el punto final de un gráfico dado y expandiéndolo más allá. Este método de extrapolación en el pronóstico proporciona buenos resultados cuando el punto a predecir no está demasiado lejos de los datos. La interpolación lineal es útil para encontrar valores entre puntos dados. Se puede considerar como "llenar los vacíos" de la tabla de datos.

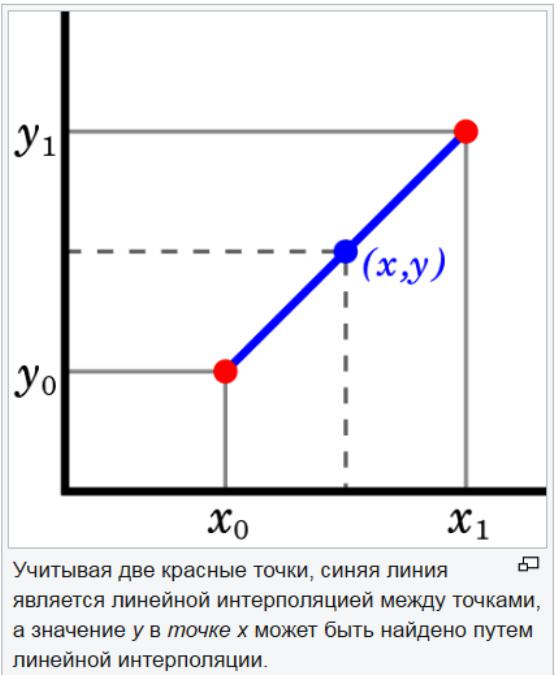
Una estrategia de interpolación lineal es usar una línea recta para conectar puntos de valores conocidos a ambos lados de lo desconocido. La interpolación lineal no es precisa para parámetros no lineales. Si los puntos en el conjunto de datos cambian en gran medida, la interpolación lineal puede dar una estimación incorrecta.

La extrapolación lineal puede ayudar a estimar valores superiores o inferiores a los valores del conjunto de datos. Su estrategia es utilizar un subconjunto de datos en lugar de todo el conjunto. Para este tipo de valor, es útil aplicar el método de extrapolación en el pronóstico utilizando los últimos dos o tres puntos para estimar un valor que excede el rango de datos.

Extracciones polinomiales y cónicas

Se sabe que tres puntos dan un polinomio único. Se puede continuar una curva polinómica después del final de dichos datos. Por lo general, se realiza mediante el método de Newton con una diferencia finita o utilizando la fórmula de interpolación de Lagrange. Un polinomio de orden superior debe extrapolarse con el debido cuidado, ya que existe una buena posibilidad de error con la extrapolación polinómica. Si esto sucede, la estimación del error aumentará exponencialmente con el grado del polinomio.

En matemáticas, la extrapolación polinómica mínima es una transformación de secuencia utilizada para acelerar la convergencia. Aunque el método de Aitken es mejor conocido, a menudo falla, especialmente para secuencias de vectores. En este caso, se realiza una iteración que construye la matriz. Sus columnas son diferencias.

Por ejemplo, se puede hacer un método de extrapolación para una sección cónica utilizando 5 puntos indicados cerca del final de los datos. En caso de que la sección cónica sea un círculo o una elipse, entonces se enrollará y se reunirá consigo misma. La parábola o la hipérbola nunca se cruzan. Pero pueden doblarse sobre el eje X. La extrapolación del cono se puede hacer en papel con una sección cónica o usando una computadora.

Método de evaluación matemática

En este método de extrapolación, se predice el valor para el período base. Las acciones descritas a continuación son realizadas automáticamente por el sistema y no son visibles para el usuario. La descripción está destinada a refinar el algoritmo, que muestra los valores esperados de la cantidad almacenada en el sistema y predice el resultado de la medición del medidor.

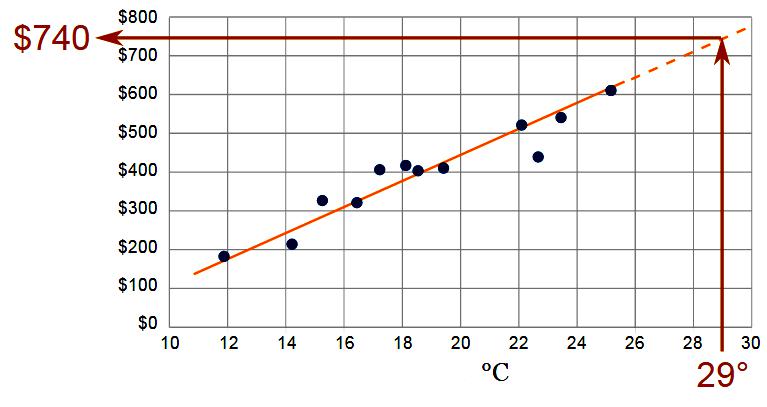
La extrapolación usando la definición de la cantidad del procedimiento se realiza usando la función: Yt = f (yi, t, aj).

Como base para la extrapolación, se agregan los datos redondeados de un período base típico almacenado en los resultados de lectura. El sistema determina el peso Yt de los datos de series de tiempo en t (tiempo del período de pronóstico) para obtener la solución correcta por extrapolación. Donde en el punto de referencia se toman yi - nivel de la serie y aj - parámetro de la ecuación de tendencia.

Predicción de funciones

El método de fijación de una curva estadística es aplicable a la predicción de la funcionalidad.Los procedimientos estadísticos corresponden a los datos pasados ​​de una o más funciones matemáticas, como lineal, logarítmica, de Fourier o exponencial. Los mejores son seleccionados por una prueba estadística. Entonces este pronóstico se extrapola de esta conexión matemática por el método de extrapolación matemática. Una de las formas más fáciles de obtener estimaciones aproximadas de las condiciones futuras (o pasadas) es extrapolar los datos que cambian con el tiempo.

Por ejemplo, si necesita hacer una evaluación aproximada de los niveles futuros de contaminantes en el agua potable con 20 años de anticipación, puede extrapolar esta tendencia de los últimos 20 años. Lo mismo se observa si necesita estimar la prevalencia del tabaquismo o el cáncer de pulmón en el fondo en el futuro. Se puede hacer un pronóstico calculando las tendencias de los últimos años. Las extrapolaciones de este tipo se pueden hacer utilizando métodos menos complejos. En muchos casos (especialmente en las áreas de marketing y gestión empresarial), el método de extrapolación se usa tradicionalmente, por ejemplo, al ver los últimos datos y evaluar intuitivamente lo que se entiende en el futuro.

Los métodos basados ​​en reglas también se pueden utilizar aplicando un conjunto de principios o expectativas predefinidos basados ​​en una comprensión preliminar del sistema y teniendo en cuenta los últimos datos para interpretar eventos futuros.

Con cualquier método de extrapolación, la precaución es importante debido a la presencia de numerosas incertidumbres. Cualquier procedimiento de extrapolación se basa en el supuesto de que hay información confiable disponible en datos y conocimientos anteriores. En consecuencia, el futuro está determinado por los mismos factores que actuaron anteriormente.

Errores de pronóstico

La falacia de la extrapolación (más precisamente, la falacia de la extrapolación injustificada) ocurre cuando el fenómeno responsable de una serie de efectos locales triviales se lee como un gran fenómeno global. Otra razón del error es que a veces las reglas generalizadas se deducen de muy pocos hechos. Por lo tanto, la teoría de la evolución de Darwin es un ejemplo fantástico de la aplicación del método de extrapolación, en el que se anuncian los mecanismos de cambios aleatorios y la selección natural para tener en cuenta el desarrollo de estructuras tan complejas como la visión de los mamíferos o el sistema inmune de los organismos vivos.

Al intentar interpretar los resultados de la investigación, el científico debe evitar la extrapolación fuera del rango de datos y tener en cuenta los supuestos subyacentes para evitar aceptar conclusiones no válidas. En general, la extrapolación es una herramienta científica legítima. Hay dos aspectos que ayudan a distinguir entre extrapolación válida y errónea. La probabilidad de extrapolación errónea es mayor cuando se obtuvieron puntos por datos insuficientes para su construcción.

Herramientas estadísticas de Excel

Para encontrar una correlación entre años y resultados (por ejemplo, en un negocio), puede usar Excel.

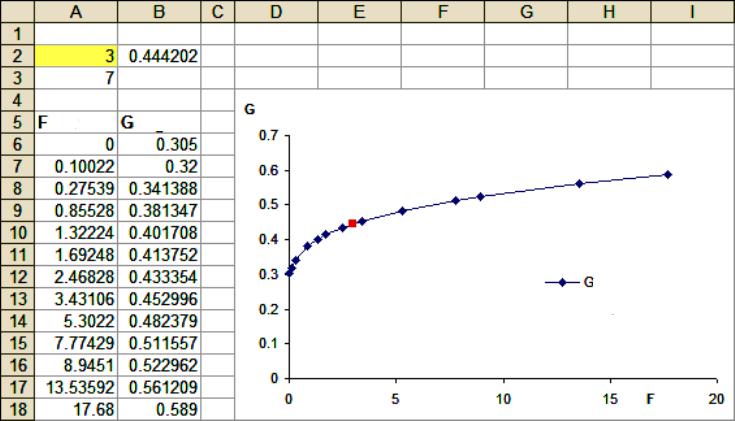
Para estas tareas, se utilizan herramientas estadísticas para el modelado de extrapolación que están integradas en todas las versiones de Excel, comenzando con 97. Procedimiento:

1. Ingrese valores conocidos, por ejemplo, ventas totales para 2016-2017, si necesita determinarlos para 2018 y 2020.
2. Instalar Analysis, una característica que requiere el uso de un complemento.
3. Para instalarlo, extraiga del menú "Herramientas", "Complementos".
4. Verifique la ventana de la utilidad de análisis y confirme con "OK".
5. Medir correlaciones entre dos series.
6. La extrapolación que debe hacerse solo tiene sentido si existe una tendencia clara (correlación) entre los dos conjuntos de números (años y ventas) por el método de extrapolación de tendencias.
7. Para medir esta correlación, use el menú "Herramientas", "Utilidades de análisis".
8. En la lista "Herramientas de análisis", seleccione "Análisis de correlación" y haga clic en "Aceptar".
9. En el campo Rango de entrada, ingrese el rango analizado, por ejemplo A6: B18, Excel agregará el símbolo "$".
10. En el área "Opciones de salida", verifique el rango de salida e ingréselo en el campo adyacente.
11. Confirmar con OK.
12. Excel crea una matriz de dos filas en dos columnas. Encuentre el valor calculado (por ejemplo, 0.981). Dado que este valor es cercano a 1, esto significa que existe una fuerte correlación entre años y cifras de ventas. Si el usuario recibe un valor cercano a cero, esto significará que la tendencia no se produce. En este caso, la extrapolación no tiene sentido.
13. Comienza una evaluación de los valores futuros.
14. Seleccione el rango requerido y haga clic en el botón "Asistente de gráficos".
15. Seleccione un gráfico (por ejemplo, nubes de puntos) y haga clic en Finalizar.

El uso de medias móviles

Estos dos métodos de extrapolación implican el uso generalizado de datos de ventas para predecir el futuro. El valor promedio móvil toma una serie de datos y "suaviza" las fluctuaciones en ellos. El objetivo es extraer extremos de datos de un período a otro. Los promedios móviles a menudo se calculan trimestralmente o semanalmente. Para predecir valores futuros, la extrapolación implica el uso de tendencias establecidas por datos históricos. La suposición principal de la extrapolación es que la muestra continuará en el futuro, a menos que la evidencia real indique lo contrario. Para comprender estos métodos con más detalle, puede considerar un cuadro que muestre las ventas de gadgets para grandes empresas de 2012 a 2015.

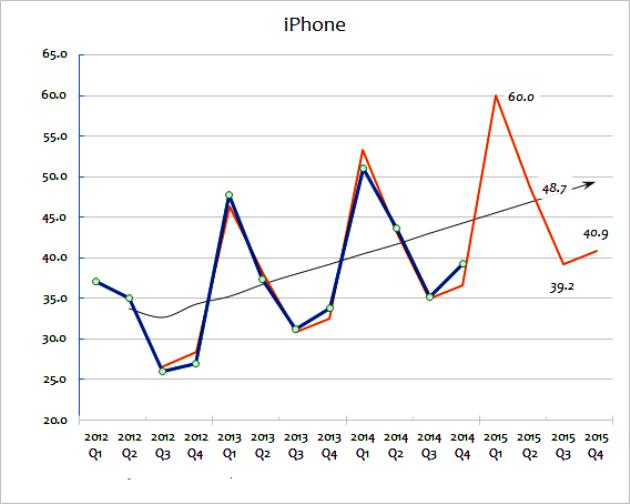
Este método de extrapolación de cálculo muestra la cifra de ventas real. Como puede ver, la cantidad total de ventas varía de año en año, aunque puede adivinar (mirando los datos) que hay una tendencia general para el crecimiento de las ventas. La línea negra muestra el promedio móvil. Esto se calcula sumando los últimos años de ventas (por ejemplo, Q1 + Q2 + Q3 + Q4) y luego dividiendo por cuatro.

Este método suaviza los cambios anuales y da una buena idea de la tendencia general en las ventas anuales. Un promedio móvil ayuda a indicar una tendencia de crecimiento, expresada como un porcentaje. Es esta extrapolación la que se usará primero para predecir el camino de las ventas futuras. Esto se puede hacer matemáticamente usando una hoja de cálculo. Alternativamente, una tendencia extrapolada puede simplemente dibujarse en un gráfico como una estimación aproximada.

Correlación de tendencia

Siempre una tecnología es la precursora de otra. Esto sucede cuando los avances realizados en la tecnología precursora pueden ser adoptados por la tecnología de seguimiento. Cuando existen tales relaciones, el conocimiento de los cambios en la tecnología de los predecesores se puede utilizar para predecir el progreso de los seguidores de la tecnología en el futuro. Además, la extrapolación del precursor permite predecir la continuación del seguimiento más allá del tiempo de retraso.

En este caso, se utiliza el método de extrapolación de tendencias, en el que, por ejemplo, se comparan las tendencias en la velocidad de los aviones militares y de transporte. Otro ejemplo de pronóstico de correlación de tendencias es predecir el tamaño y la potencia de las computadoras futuras en función de los avances en la tecnología microelectrónica. A veces, la tecnología de los seguidores depende de varias tecnologías de precursores, pero no de un predecesor.

Las combinaciones fijas de predecesores pueden afectar el cambio en la secuencia, pero más a menudo las combinaciones no son fijas, y las entradas de los predecesores difieren tanto en combinación como en fuerza. Por ejemplo, un aumento en la velocidad de la aeronave puede ocurrir debido a la mejora de motores, materiales, controles, combustible, aerodinámica y varias combinaciones de estos factores.

Un ejemplo de un pronóstico de correlación obtenido al extrapolar las tendencias: millas totales de pasajeros, millas geográficas totales y potencia de aterrizaje promedio.La extrapolación de tendencias estadísticamente determinadas permite un enfoque objetivo para el pronóstico. Sin embargo, este enfoque tiene serias limitaciones y dificultades. Cualquier error o elección incorrecta realizada en la determinación de los datos históricos se reflejará en el pronóstico, lo que reduce su valor.

Aplicaciones, atributos y límites

El método de extrapolación pertenece al campo de pronóstico. Sugiere que los patrones que existieron en el pasado continuarán en el futuro, y que estos patrones son regulares y pueden medirse. En otras palabras, el pasado es un buen indicador del futuro. Las aplicaciones son útiles para desarrollar datos de referencia.

Los atributos y límites son herramientas de cálculo simples y baratas, así como modelos teóricos complejos.

1. Datos de proceso: gráficos y observaciones.
2. La clave es tener una buena base de datos y comprender la estructura dentro de ella.
3. La técnica es el mejor ajuste, relación, etc.

Los procedimientos estadísticos estándar temporales no conducen a una selección precisa de tendencias que el pronosticador puede extrapolar con comodidad, realizando el pronóstico por extrapolación. En tales casos, el pronosticador puede "ajustar" los resultados estadísticos utilizando el juicio. También puede ignorar completamente las estadísticas y extrapolar toda la tendencia basada en el juicio.

Los pronósticos generados de esta manera son menos precisos que los pronósticos estadísticos, pero no necesariamente insatisfactorios. Un ejemplo de tal extrapolación de una tendencia de calidad es predecir la complejidad del avión. Los intentos de cuantificar esta tendencia no han tenido éxito. Pero el porcentaje de partes móviles o ajustables de la aeronave fue extrapolado con la frecuencia con la cual tales elementos fueron introducidos en el pasado. Estas previsiones fueron bastante precisas.

Los cambios técnicos específicos no pueden predecirse de esta manera, pero sí el grado de cambio. Esto proporciona materiales de planificación útiles, que indican una tendencia en el comportamiento pasado.