Das zusammengesetzte Wort "Extrapolation" besteht aus zwei einfachen Wörtern. Das erste Wort in lateinischer Sprache klingt extra und bedeutet "draußen", "für", "draußen". Die zweite in demselben Latein klingt polirisch und bedeutet "ändern", "begradigen", "glatt". Im Allgemeinen kann die Extrapolation als ein Wert außerhalb von zwei gegebenen Punkten definiert werden. Es wird eine Bewertung dessen betrachtet, was aus bekannten Fakten extrahiert wird, die Daten in einem unbekannten Bereich erweitern, um zu dem beabsichtigten Ergebnis zu gelangen. Dieses Konzept kann auch auf die Vorhersage des Bildes der Zukunft zurückgeführt werden, wobei die Wahrheit über gegenwärtige und vergangene Trends vorausgesetzt wird.
Die Extrapolationsmethode geht davon aus, dass Daten oder Beobachtungen auch in Zukunft ähnlich sind. Somit können zukünftige Ergebnisse vorhergesagt werden. Es kann als mathematische Hypothese angesehen werden. Die Extrapolation verwendet die Daten und Fakten einer bestimmten Situation und liefert Vorhersagen darüber, was am Ende passieren kann.
Hochrechnungshistorie

Diese Methode wird oft als Richardson-Extrapolation oder Romberg-Methode bezeichnet. Dies ist jedoch nicht ganz richtig, da es seit Jahrhunderten ähnliche numerische Methoden zur Lösung solcher Probleme gibt. Daher ist der berühmte Richardson h2 (Extrapolation für eine numerische Lösung) nicht der erste. Eine ähnliche Methode war bereits 1654 in Huygens-Rechnungen anwendbar. Der Begriff "Extrapolation" selbst wurde erstmals 1959 von Thomas D. Clareson in einem Buch über Wissenschaft und Fiktion geprägt.
Extrapolationsmethoden können als Erweiterung von Daten oder Prozessen verstanden werden, was darauf hindeutet, dass ein ähnlicher Prozess außerhalb von Daten oder Prozessen angewendet wird. Extrapolation ist ein wichtiges Konzept, das nicht nur in der Mathematik, sondern auch in anderen Bereichen wie Soziologie, Psychologie und Prognose angewendet wird. Beispielsweise extrapoliert ein Fahrer normalerweise Fahrbedingungen außerhalb seiner Sicht. Die Extrapolation kann auf eine Methode zurückgeführt werden, bei der Datenwerte als Punkte x1, x2 ..., xn behandelt werden und der Wert sich dann der Grenze eines bestimmten Punktebereichs nähert.
Vorteile der Verwendung:
- Eine einfache Prognosemethode.
- Es sind nicht viele Daten erforderlich.
- Schnelle und kostengünstige Analyse.
Die Methode existiert in der Statistik. Wenn periodisch Werte entfernt werden, nähert sich die Antwort dem nächsten Datenpunkt. Ein Beispiel für eine Extrapolationsmethode ist eine Wettervorhersage, die den Hintergrund der Daten untersucht und das vorhergesagte Modell der Zukunft extrapoliert. Ein noch einfacheres Beispiel: Wenn Sie Informationen zu Sonntagen, Montagen und Dienstagen haben, können Sie Mittwoch oder Donnerstag extrapolieren.
Nachteile der Verwendung von Extrapolation:
- Unzuverlässigkeit bei erheblichen Schwankungen der historischen Daten.
- Die Annahme, dass sich der vergangene Trend in Zukunft fortsetzen wird, ist in vielen wettbewerbsintensiven Geschäftsumfeldern kaum möglich.
- Ignoriert Qualitätsfaktoren wie Geschmacks- und Modeveränderungen.
Sequenzbeschleunigung
Die Extrapolationsmethode besteht darin, am Ende bekannter Daten eine Tangentenlinie zu erstellen und über diesen Bereich hinaus zu erweitern. Wie bei der Interpolation werden bei der Extrapolation viele Methoden verwendet, bei denen Vorkenntnisse über den Prozess zum Erstellen der vorhandenen Datenpunkte erforderlich sind. Die Methode umfasst lineare und polynomielle Extrapolation, konische und französische Kurvenextrapolation.
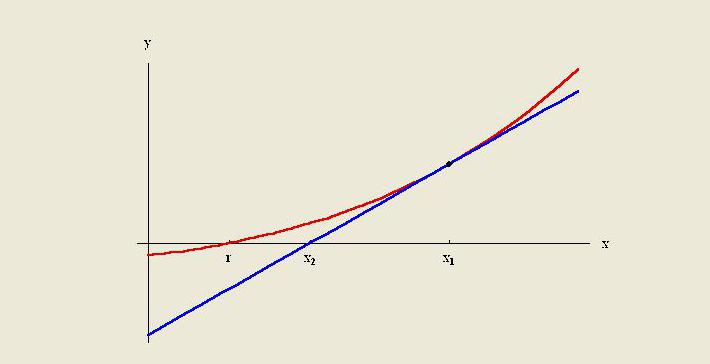
In der Regel wird die Qualität einer bestimmten Methode durch Annahmen über die Funktion eingeschränkt. In der numerischen Analyse ist die Richardson-Extrapolation eine Sequenzbeschleunigungsmethode zur Verbesserung der Konvergenzrate.Es ist nach Lewis Fry Richardson benannt. Er führte die Rechentechnik zu Beginn des 20. Jahrhunderts ein, deren Nützlichkeit für praktische Berechnungen kaum zu überschätzen ist.
Praktische Anwendungen der Richardson-Extrapolation umfassen die Romberg-Integration, die sie auf die Trapezregel und den Bulliers-Stoehr-Algorithmus anwendet, um gewöhnliche Differentialgleichungen zu lösen.
Lineare Methode
Die lineare Extrapolationsmethode ist nützlich, wenn eine lineare Funktion angegeben wird. Dazu wird eine Tangentenlinie am Endpunkt eines bestimmten Diagramms gezeichnet und über diesen Punkt hinaus erweitert. Diese Methode der Extrapolation bei der Vorhersage liefert gute Ergebnisse, wenn der vorherzusagende Punkt nicht zu weit von den Daten entfernt ist. Die lineare Interpolation ist nützlich, um Werte zwischen bestimmten Punkten zu ermitteln. Dies kann als "Ausfüllen der Lücken" der Datentabelle angesehen werden.
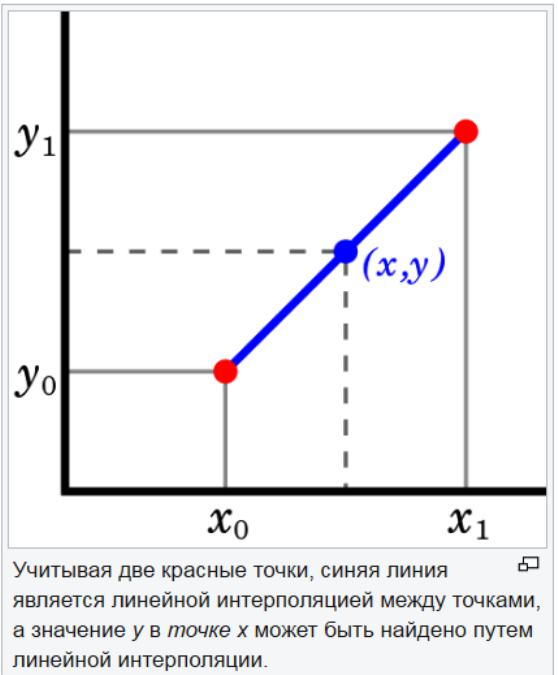
Eine lineare Interpolationsstrategie besteht darin, eine gerade Linie zu verwenden, um bekannte Wertepunkte auf beiden Seiten des Unbekannten zu verbinden. Die lineare Interpolation ist für nicht lineare Parameter nicht genau. Wenn sich die Punkte im Datensatz stark ändern, kann die lineare Interpolation zu einer falschen Schätzung führen.
Durch lineare Extrapolation können Werte geschätzt werden, die über oder unter den Werten im Datensatz liegen. Seine Strategie besteht darin, eine Teilmenge der Daten anstelle der gesamten Menge zu verwenden. Für diesen Wertetyp ist es hilfreich, die Extrapolationsmethode bei der Vorhersage unter Verwendung der letzten zwei oder drei Punkte anzuwenden, um einen Wert zu schätzen, der den Datenbereich überschreitet.
Polynom- und konische Extrapolation
Es ist bekannt, dass drei Punkte ein eindeutiges Polynom ergeben. Eine Polynomkurve kann nach dem Ende solcher Daten fortgesetzt werden. Sie wird normalerweise nach der Newton-Methode mit endlicher Differenz oder nach der Lagrange-Interpolationsformel durchgeführt. Ein Polynom höherer Ordnung sollte mit der gebotenen Sorgfalt extrapoliert werden, da bei der Polynomextrapolation eine angemessene Fehlerwahrscheinlichkeit besteht. In diesem Fall steigt die Fehlerschätzung mit dem Grad des Polynoms exponentiell an.
In der Mathematik ist die minimale Polynomextrapolation eine Sequenztransformation, die zur Beschleunigung der Konvergenz verwendet wird. Obwohl die Methode von Aitken am bekanntesten ist, versagt sie häufig, insbesondere bei Vektorsequenzen. In diesem Fall wird eine Iteration durchgeführt, die die Matrix erstellt. Seine Spalten sind Unterschiede.

Beispielsweise kann eine Extrapolationsmethode für einen konischen Abschnitt unter Verwendung von 5 Punkten durchgeführt werden, die am Ende der Daten angegeben sind. Wenn der konische Abschnitt ein Kreis oder eine Ellipse ist, wird er zurückgeschleift und mit sich selbst wieder vereint. Parabel oder Hyperbel kreuzen sich nie. Sie können jedoch auch um die X-Achse zurückgebogen werden. Die Extrapolation des Kegels kann auf Papier mit einem konischen Querschnitt oder mit einem Computer erfolgen.
Mathematische Bewertungsmethode
Bei dieser Extrapolationsmethode wird der Wert für die Basisperiode vorhergesagt. Die nachfolgend beschriebenen Aktionen werden vom System automatisch ausgeführt und sind für den Benutzer nicht sichtbar. Die Beschreibung soll den Algorithmus verfeinern, der die erwarteten Werte aus der im System gespeicherten Menge anzeigt und das Ergebnis der Zählermessung vorhersagt.
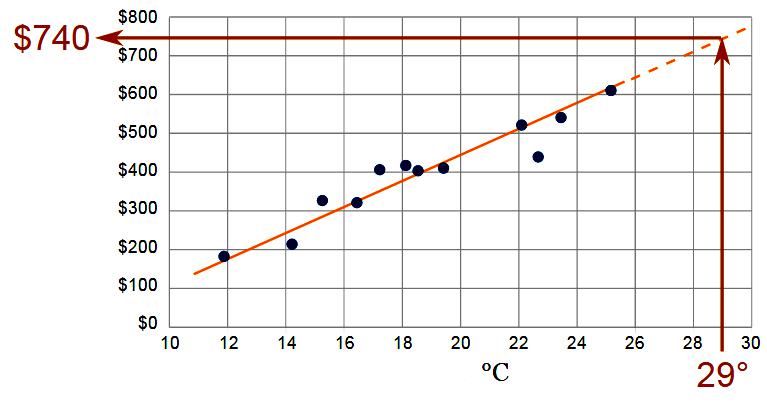
Die Extrapolation unter Verwendung der Definition des Betrags des Verfahrens wird unter Verwendung der Funktion durchgeführt: Yt = f (yi, t, aj).
Als Grundlage für die Extrapolation werden die gerundeten Daten einer typischen Basisperiode, die in den Leseergebnissen gespeichert sind, hinzugefügt. Das System ermittelt das Gewicht Yt der Zeitreihendaten in t (Zeitpunkt des Prognosezeitraums), um durch Extrapolation die richtige Lösung zu erhalten. Wo am Bezugspunkt genommen wird yi - das Niveau der Reihe und aj - der Parameter der Trendgleichung.
Feature-Vorhersage
Die Methode zum Festlegen einer statistischen Kurve ist auf die Vorhersage der Funktionalität anwendbar.Statistische Prozeduren entsprechen den Vergangenheitsdaten einer oder mehrerer mathematischer Funktionen, z. B. linear, logarithmisch, Fourier oder exponentiell. Die besten werden durch einen statistischen Test ausgewählt. Diese Prognose wird dann aus diesem mathematischen Zusammenhang mit der Methode der mathematischen Extrapolation extrapoliert. Eine der einfachsten Möglichkeiten, grobe Schätzungen der zukünftigen (oder vergangenen) Bedingungen zu erhalten, besteht darin, Daten zu extrapolieren, die sich im Laufe der Zeit ändern.
Wenn Sie beispielsweise im Voraus 20 Jahre lang eine grobe Einschätzung des zukünftigen Schadstoffgehalts im Trinkwasser vornehmen müssen, können Sie diesen Trend aus den letzten 20 Jahren extrapolieren. Das Gleiche gilt, wenn Sie die Prävalenz von Rauchen oder Lungenkrebs in Zukunft im Hintergrund abschätzen müssen. Eine Prognose kann durch Berechnung der Trends der letzten Jahre erstellt werden. Extrapolationen dieser Art können mit weniger komplexen Methoden durchgeführt werden. In vielen Fällen (insbesondere in den Bereichen Marketing und Unternehmensführung) wird die Extrapolationsmethode traditionell angewendet, indem beispielsweise die neuesten Daten angezeigt und intuitiv bewertet werden, was in Zukunft gemeint ist.
Regelbasierte Methoden können auch verwendet werden, indem eine Reihe vordefinierter Prinzipien oder Erwartungen angewendet werden, die auf einem vorläufigen Verständnis des Systems basieren und die neuesten Daten zur Interpretation zukünftiger Ereignisse berücksichtigen.
Bei jeder Extrapolationsmethode ist aufgrund der zahlreichen Unsicherheiten Vorsicht geboten. Jedes Extrapolationsverfahren basiert auf der Annahme, dass verlässliche Informationen in früheren Daten und Kenntnissen verfügbar sind. Folglich wird die Zukunft von denselben Faktoren bestimmt, die zuvor gehandelt haben.
Prognosefehler
Der Irrtum der Extrapolation (genauer der Irrtum der ungerechtfertigten Extrapolation) tritt auf, wenn das Phänomen, das für eine Reihe von geringfügigen lokalen Effekten verantwortlich ist, als großes globales Phänomen angesehen wird. Ein weiterer Grund für den Fehler ist, dass manchmal verallgemeinerte Regeln aus zu wenigen Fakten abgeleitet werden. So ist Darwins Evolutionstheorie ein fantastisches Beispiel für die Anwendung der Extrapolationsmethode, bei der die Mechanismen zufälliger Änderungen und natürlicher Selektion bekannt gegeben werden, um die Entwicklung derart komplexer Strukturen wie das Sehvermögen von Säugetieren oder das Immunsystem lebender Organismen zu berücksichtigen.
Bei dem Versuch, Forschungsergebnisse zu interpretieren, sollte der Wissenschaftler eine Extrapolation außerhalb des Datenbereichs vermeiden und die zugrunde liegenden Annahmen berücksichtigen, um zu vermeiden, dass ungültige Schlussfolgerungen akzeptiert werden. Im Allgemeinen ist die Extrapolation ein legitimes wissenschaftliches Instrument. Es gibt zwei Aspekte, die dabei helfen, zwischen einer gültigen und einer fehlerhaften Extrapolation zu unterscheiden. Die Wahrscheinlichkeit einer fehlerhaften Extrapolation ist höher, wenn Punkte für unzureichende Daten für ihre Konstruktion erhalten wurden.
Excel Statistical Tools
Mit Excel können Sie eine Korrelation zwischen Jahren und Ergebnissen finden (z. B. in einem Unternehmen).
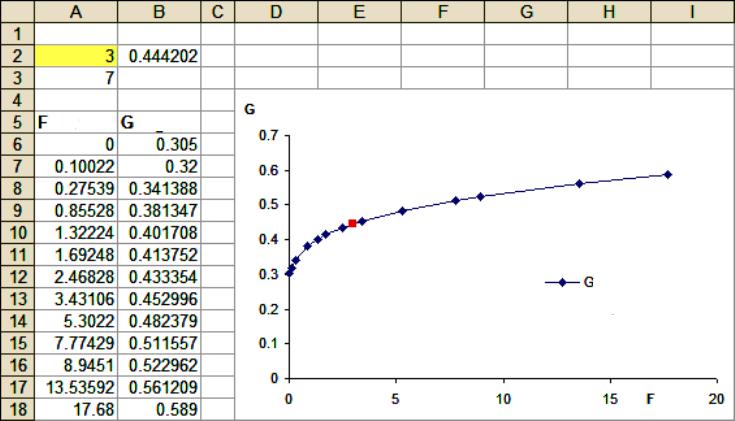
Für diese Aufgaben werden statistische Tools für die Extrapolationsmodellierung verwendet, die in alle Excel-Versionen integriert sind, beginnend mit 97. Vorgehensweise:
- Geben Sie bekannte Werte ein, z. B. den Gesamtumsatz für 2016-2017, wenn Sie diese für 2018 und 2020 ermitteln müssen.
- Installieren Sie Analysis, eine Funktion, die die Verwendung eines Add-Ins erfordert.
- Um es zu installieren, extrahieren Sie aus dem Menü "Extras" "Add-Ons".
- Überprüfen Sie das Analyse-Utility-Fenster und bestätigen Sie mit „OK“.
- Korrelationen zwischen zwei Reihen messen.
- Die Extrapolation, die durchgeführt werden muss, ist nur sinnvoll, wenn ein eindeutiger Trend (Korrelation) zwischen den beiden Mengen von Zahlen (Jahren und Umsätzen) durch die Methode der Extrapolation von Trends vorliegt.
- Um diese Korrelation zu messen, verwenden Sie das Menü "Tools", "Analysis Utilities".
- Wählen Sie in der Liste „Analyse-Tools“ die Option „Korrelationsanalyse“ und klicken Sie auf „OK“.
- Geben Sie im Feld Eingabebereich den analysierten Bereich ein, z. B. A6: B18. Excel fügt das Symbol "$" hinzu.
- Überprüfen Sie im Bereich "Ausgabeoptionen" den Ausgabebereich und geben Sie ihn in das nebenstehende Feld ein.
- Bestätigen Sie mit OK.
- Excel erstellt ein Array von zwei Zeilen in zwei Spalten. Suchen Sie den berechneten Wert (z. B. 0,981). Da dieser Wert nahe 1 liegt, besteht eine starke Korrelation zwischen den Jahren und den Verkaufszahlen. Wenn der Benutzer einen Wert nahe Null erhält, bedeutet dies, dass der Trend nicht auftritt. In diesem Fall ist eine Hochrechnung nicht sinnvoll.
- Eine Bewertung zukünftiger Werte beginnt.
- Wählen Sie den gewünschten Bereich und klicken Sie auf die Schaltfläche "Diagramm-Assistent".
- Wählen Sie ein Diagramm aus (z. B. Punktwolken) und klicken Sie auf Fertig stellen.
Die Verwendung von gleitenden Durchschnitten
Diese beiden Extrapolationsmethoden beinhalten die weit verbreitete Verwendung von Verkaufsdaten, um die Zukunft vorherzusagen. Der gleitende Mittelwert nimmt eine Reihe von Daten auf und "gleicht" Schwankungen darin aus. Ziel ist es, Datenextreme von Periode zu Periode zu extrahieren. Die gleitenden Durchschnitte werden häufig vierteljährlich oder wöchentlich berechnet. Zur Vorhersage zukünftiger Werte werden bei der Extrapolation Trends verwendet, die anhand historischer Daten ermittelt wurden. Bei der Extrapolation wird hauptsächlich davon ausgegangen, dass die Stichprobe auch in Zukunft fortgeführt wird, sofern die tatsächlichen Beweise nichts anderes angeben. Um diese Methoden genauer zu verstehen, können Sie ein Diagramm betrachten, das den Umsatz von Gadgets für große Unternehmen von 2012 bis 2015 zeigt.
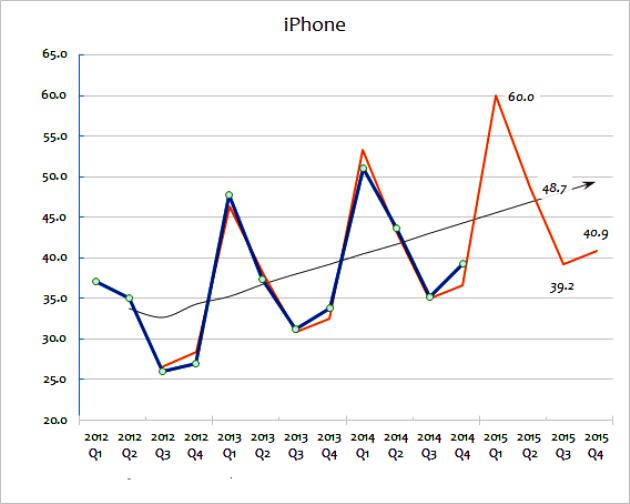
Diese Berechnungsextrapolationsmethode zeigt den tatsächlichen Umsatz. Wie Sie sehen, variiert die Gesamtmenge der Verkäufe von Jahr zu Jahr, obwohl Sie (anhand der Daten) davon ausgehen können, dass es einen allgemeinen Trend für das Umsatzwachstum gibt. Die schwarze Linie zeigt den gleitenden Durchschnitt. Dies wird berechnet, indem die letzten Verkaufsjahre (z. B. Q1 + Q2 + Q3 + Q4) addiert und dann durch vier dividiert werden.
Diese Methode gleicht jährliche Veränderungen aus und gibt einen guten Überblick über die allgemeine Entwicklung des Jahresumsatzes. Ein gleitender Durchschnitt zeigt einen Wachstumstrend in Prozent an. Es ist diese Extrapolation, die zuerst verwendet wird, um den Weg zukünftiger Verkäufe vorherzusagen. Dies kann mathematisch mithilfe einer Kalkulationstabelle erfolgen. Alternativ kann ein extrapolierter Trend einfach als grobe Schätzung in ein Diagramm eingetragen werden.
Trendkorrelation
Immer ist eine Technologie der Vorläufer einer anderen. Dies geschieht, wenn die in der Vorläufertechnologie erzielten Fortschritte von der Folgetechnologie übernommen werden können. Wenn solche Beziehungen bestehen, kann das Wissen über Änderungen in der Technologie von Vorgängern verwendet werden, um den Fortschritt von Technologie-Followern in der Zukunft vorherzusagen. Zusätzlich ermöglicht die Extrapolation des Vorläufers die Vorhersage der Fortsetzung der Verfolgung über die Zeitverzögerung hinaus.
In diesem Fall wird die Methode der Extrapolation von Trends verwendet, bei der beispielsweise die Trends in der Geschwindigkeit von Militär- und Transportflugzeugen verglichen werden. Ein weiteres Beispiel für die Vorhersage von Trendkorrelationen ist die Vorhersage der Größe und Leistung zukünftiger Computer auf der Grundlage der Fortschritte in der Mikroelektroniktechnologie. Manchmal hängt die Technologie von Followern von mehreren Technologien von Vorläufern ab, aber nicht von einem Vorgänger.
Feste Kombinationen von Vorgängern können sich auf die Änderung der Reihenfolge auswirken, häufiger sind die Kombinationen jedoch nicht festgelegt, und die Eingaben der Vorgänger unterscheiden sich sowohl in Kombination als auch in Stärke. Beispielsweise kann eine Erhöhung der Flugzeuggeschwindigkeit aufgrund der Verbesserung von Motoren, Materialien, Steuerungen, Kraftstoff, Aerodynamik und verschiedenen Kombinationen dieser Faktoren auftreten.
Ein Beispiel für eine Korrelationsprognose, die durch Extrapolation der Trends erhalten wird: Gesamtzahl der Passagiermeilen, Gesamtzahl der geografischen Meilen und durchschnittliche Landeleistung.Die Extrapolation statistisch ermittelter Trends ermöglicht einen objektiven Ansatz für die Vorhersage. Dieser Ansatz weist jedoch schwerwiegende Einschränkungen und Fallstricke auf. Alle Fehler oder falschen Auswahlen bei der Ermittlung historischer Daten werden in der Prognose berücksichtigt, wodurch sich ihr Wert verringert.
Anwendungen, Attribute und Grenzen
Die Extrapolationsmethode gehört zum Bereich der Prognose. Er schlägt vor, dass Muster, die in der Vergangenheit existierten, auch in der Zukunft fortbestehen, und dass diese Muster regelmäßig sind und gemessen werden können. Mit anderen Worten, die Vergangenheit ist ein guter Indikator für die Zukunft. Anwendungen sind nützlich für die Entwicklung von Basisdaten.
Attribute und Grenzen sind einfache und kostengünstige Berechnungswerkzeuge sowie komplexe theoretische Modelle.
- Prozessdaten - Grafiken und Beobachtungen.
- Der Schlüssel ist, eine gute Datenbank zu haben und die Struktur darin zu verstehen.
- Die Technik ist die beste Passform, das beste Verhältnis usw.
Temporäre statistische Standardverfahren führen nicht zu einer genauen Auswahl von Trends, die der Prognostiker bequem extrapolieren und die Prognose durch Extrapolation durchführen kann. In solchen Fällen kann der Prognostiker die statistischen Ergebnisse mithilfe von Beurteilungen „anpassen“. Es kann auch Statistiken vollständig ignorieren und den gesamten Trend basierend auf der Beurteilung extrapolieren.
Auf diese Weise erstellte Vorhersagen sind weniger genau als statistische Vorhersagen, aber nicht unbedingt unbefriedigend. Ein Beispiel für eine solche Hochrechnung eines Qualitätstrends ist die Vorhersage der Flugzeugkomplexität. Versuche, diesen Trend zu quantifizieren, waren nicht erfolgreich. Der Prozentsatz der beweglichen oder einstellbaren Teile des Flugzeugs wurde jedoch mit der Häufigkeit extrapoliert, mit der solche Elemente in der Vergangenheit eingeführt wurden. Diese Vorhersagen waren ziemlich genau.
Spezifische technische Änderungen können auf diese Weise nicht vorhergesagt werden, der Grad der Änderung jedoch. Dies bietet nützliche Planungsmaterialien, die auf einen Trend im Verhalten der Vergangenheit hinweisen.
