Korrelations-Regressions-Analyse - Dies ist eine der häufigsten Methoden zur Untersuchung der Beziehung zwischen numerischen Werten. Ihr Hauptziel ist es, die Beziehung zwischen den beiden Parametern und ihrem Grad mit der anschließenden Herleitung der Gleichung zu finden. Zum Beispiel haben wir Studenten, die die Mathematik- und Englischprüfung bestanden haben. Mithilfe der Korrelation können wir feststellen, ob der Erfolg eines Tests die Ergebnisse eines anderen Probanden beeinflusst. In Bezug auf die Regressionsanalyse ist es hilfreich, die Mathematiknoten anhand der in einer Englischprüfung erzielten Punkte vorherzusagen und umgekehrt.

Was ist ein Korrelationsdiagramm?
Jede Analyse beginnt mit der Erfassung von Informationen. Je mehr es ist, desto genauer ist das am Ende erzielte Ergebnis. Im obigen Beispiel haben wir zwei Disziplinen, in denen die Schüler eine Prüfung bestehen müssen. Ihre Erfolgsquote ist eine Schätzung. Die Korrelations-Regressions-Analyse zeigt, ob das Ergebnis eines Probanden die in der zweiten Prüfung erzielten Punkte beeinflusst. Um diese Frage beantworten zu können, müssen die Bewertungen aller Studierenden parallel analysiert werden. Aber zuerst müssen Sie sich für die abhängige Variable entscheiden. In diesem Fall ist es nicht so wichtig. Angenommen, eine Mathematikprüfung hat früher stattgefunden. Punkte darauf sind eine unabhängige Variable (sie werden entlang der Abszisse verschoben). Englisch steht später auf dem Stundenplan. Schätzungen, die darauf basieren, sind daher eine abhängige Variable (sind entlang der Ordinate aufgetragen). Je mehr das so erhaltene Diagramm wie eine gerade Linie aussieht, desto stärker ist die lineare Korrelation zwischen den beiden ausgewählten Werten. Dies bedeutet, dass Studenten der Mathematik häufiger Fünfer in der Englischprüfung werden.
Annahmen und Vereinfachungen
Die Methode der Korrelations- und Regressionsanalyse beinhaltet das Finden eines Kausalzusammenhangs. In der ersten Phase müssen Sie jedoch verstehen, dass Änderungen in beiden Größen auf ein Drittel zurückzuführen sein können, das der Forscher noch nicht berücksichtigt hat. Es kann auch nichtlineare Beziehungen zwischen den Variablen geben. Daher ist das Erhalten eines Koeffizienten von Null nicht das Ende des Experiments.
Pearson lineare Korrelation
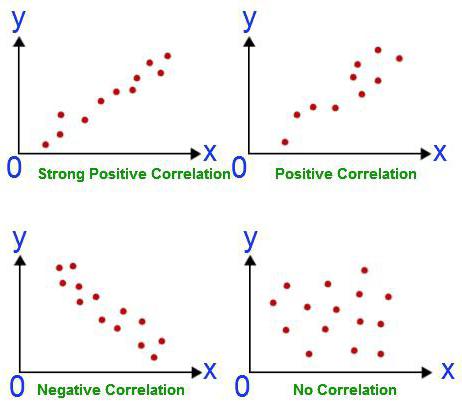
Dieser Koeffizient kann unter zwei Bedingungen verwendet werden. Der erste - alle Werte der Variablen sind rationale Zahlen, der zweite - es wird erwartet, dass sich die Werte proportional ändern. Dieser Koeffizient liegt immer zwischen -1 und 1. Ist er größer als Null, so besteht eine direkt proportionale Abhängigkeit, weniger - umgekehrt - gleich - diese Werte beeinflussen sich in keiner Weise gegenseitig. Die Fähigkeit, diesen Indikator zu berechnen, ist die Grundlage für die Korrelations- und Regressionsanalyse. Zum ersten Mal wurde dieser Koeffizient von Karl Pearson auf der Grundlage der Idee von Francis Galton entwickelt.
Eigenschaften und Vorsichtsmaßnahmen
Der Pearson-Korrelationskoeffizient ist ein leistungsfähiges Werkzeug, sollte aber auch mit Vorsicht angewendet werden. Die folgenden Warnungen werden verwendet:
- Der Pearson-Koeffizient gibt das Vorhandensein oder Fehlen einer linearen Beziehung an. Die Korrelations-Regressions-Analyse endet hier nicht, es kann sich herausstellen, dass die Variablen dennoch miteinander verbunden sind.
- Bei der Interpretation des Koeffizienten muss man vorsichtig sein. Eine Korrelation kann zwischen Beingröße und IQ-Level gefunden werden.Dies bedeutet jedoch nicht, dass ein Indikator einen anderen bestimmt.
- Der Pearson-Koeffizient sagt nichts über den Kausalzusammenhang zwischen den Indikatoren aus.

Rangkorrelationskoeffizient nach Spearman
Wenn eine Änderung des Wertes eines Indikators zu einer Erhöhung oder Verringerung des Wertes eines anderen Indikators führt, bedeutet dies, dass sie miteinander zusammenhängen. Die Korrelations-Regressions-Analyse, von der im Folgenden ein Beispiel gegeben wird, ist genau mit solchen Parametern verbunden. Mit dem Rangkoeffizienten können Sie die Berechnungen vereinfachen.
Korrelations- und Regressionsanalyse: ein Beispiel
Angenommen, es gibt eine Bewertung der Wirksamkeit von zehn Unternehmen. Wir haben zwei Richter, die ihnen Punkte geben. Die Korrelations- und Regressionsanalyse des Unternehmens kann in diesem Fall nicht auf der Grundlage des linearen Pearson-Koeffizienten durchgeführt werden. Wir sind nicht an der Beziehung zwischen den Richterbewertungen interessiert. Die Reihen der Unternehmen sind nach Ansicht der Richter wichtig.
Diese Art der Analyse hat folgende Vorteile:
- Nichtparametrische Form der Beziehungen zwischen den untersuchten Größen.
- Einfache Bedienung, da die Ränge sowohl in aufsteigender als auch in absteigender Reihenfolge zugeordnet werden können.
Die einzige Voraussetzung für diese Art der Analyse ist die Konvertierung der Quelldaten.
Anwendungsprobleme
Die Korrelations- und Regressionsanalyse basiert auf folgenden Annahmen:
- Beobachtungen gelten als unabhängig (ein fünffacher Verlust des „Adlers“ hat keinen Einfluss auf das Ergebnis des nächsten Münzwurfs).
- In der Korrelationsanalyse werden beide Variablen als zufällig betrachtet. In der Regression - nur eine (abhängig).
- Beim Testen einer Hypothese muss eine Normalverteilung eingehalten werden. Die Änderung der abhängigen Variablen sollte für jeden Wert auf der Abszisse gleich sein.
- Das Korrelationsdiagramm ist nur der erste Test der Hypothese über die Beziehung zwischen den beiden Parameterreihen und nicht das Endergebnis der Analyse.
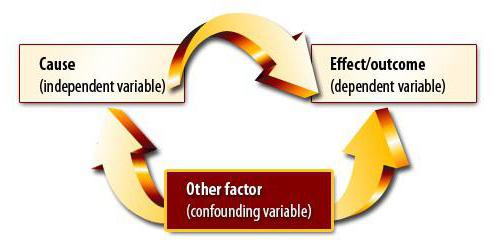
Abhängigkeit und Kausalität
Angenommen, wir haben den Korrelationskoeffizienten von Exportvolumen und BIP berechnet. Es stellte sich heraus, dass dies gleichbedeutend mit Unity Modulo ist. Haben wir Korrelations- und Regressionsanalysen bis zum Ende durchgeführt? Natürlich nicht. Das erzielte Ergebnis bedeutet keineswegs, dass das BIP durch den Export ausgedrückt werden kann. Wir haben noch keinen kausalen Zusammenhang zwischen Indikatoren nachgewiesen. Korrelations-Regressions-Analyse - Vorhersage der Werte einer Variablen basierend auf einer anderen. Sie müssen jedoch verstehen, dass oft viele Faktoren den Parameter beeinflussen. Der Export bestimmt das BIP, aber nicht nur das. Es gibt noch andere Faktoren. Hier besteht eine Korrelation und ein Kausalzusammenhang, allerdings bereinigt um andere Komponenten des Bruttoinlandsprodukts.
Eine andere Situation ist viel gefährlicher. In Großbritannien wurde eine Umfrage durchgeführt, die ergab, dass Kinder, deren Eltern rauchten, häufiger Straftäter waren. Diese Schlussfolgerung basiert auf einer starken Korrelation zwischen dem Indikator. Aber hat er recht? Erstens könnte die Abhängigkeit umgekehrt sein. Eltern könnten mit dem Rauchen anfangen, weil ihre Kinder sich ständig verändern und gegen das Gesetz verstoßen. Zweitens können beide Parameter auf den dritten zurückzuführen sein. Solche Familien gehören niedrigen sozialen Schichten an, die durch beide Probleme gekennzeichnet sind. Aufgrund der Korrelation kann daher nicht auf einen Kausalzusammenhang geschlossen werden.
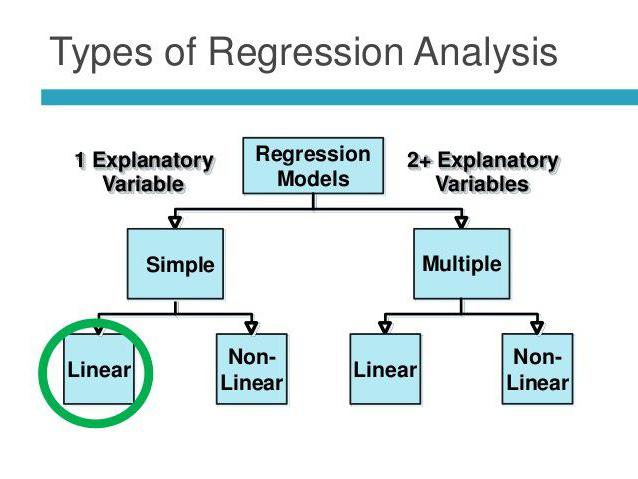
Warum Regressionsanalyse verwenden?
Korrelationsabhängigkeit beinhaltet das Finden von Beziehungen zwischen Größen. Der Kausalzusammenhang bleibt in diesem Fall hinter den Kulissen. Die Aufgaben der Korrelations- und Regressionsanalyse fallen nur insoweit zusammen, als die Existenz einer Beziehung zwischen den Werten zweier Größen bestätigt wird. Zunächst achtet der Forscher jedoch nicht auf die Möglichkeit eines Kausalzusammenhangs. Die Regressionsanalyse hat immer zwei Variablen, von denen eine abhängig ist. Es findet in mehreren Phasen statt:
- Auswahl des richtigen Modells nach der Methode der kleinsten Quadrate.
- Herleitung einer Gleichung, die die Auswirkung einer Änderung einer unabhängigen Variablen auf eine andere beschreibt.
Wenn wir zum Beispiel die Auswirkung des Alters auf das menschliche Wachstum untersuchen, kann eine Regressionsanalyse dazu beitragen, Veränderungen im Laufe der Jahre vorherzusagen.
Lineare und multiple Regression
Angenommen, X und Y sind zwei verwandte Variablen. Die Regressionsanalyse ermöglicht es uns, die Größe eines von ihnen basierend auf den Werten des anderen vorherzusagen. Zum Beispiel sind Reife und Alter abhängige Symptome. Die Beziehung zwischen ihnen wird durch lineare Regression wiedergegeben. Tatsächlich können Sie X durch Y oder umgekehrt ausdrücken. Oft ist jedoch nur eine der Regressionsgeraden korrekt. Der Erfolg der Analyse hängt wesentlich von der korrekten Bestimmung der unabhängigen Variablen ab. Zum Beispiel haben wir zwei Indikatoren: Ertrag und Niederschlag. Aus der alltäglichen Erfahrung wird deutlich, dass die erste von der zweiten abhängt und nicht umgekehrt.
Mit der multiplen Regression können Sie einen unbekannten Wert basierend auf den Werten von drei oder mehr Variablen berechnen. Beispielsweise hängt der Reisertrag pro Hektar Land von der Kornqualität, der Bodenfruchtbarkeit, den Düngemitteln, der Temperatur und den Niederschlägen ab. Alle diese Parameter beeinflussen das Gesamtergebnis. Zur Vereinfachung des Modells werden die folgenden Annahmen verwendet:
- Die Beziehung zwischen unabhängigen und beeinflussenden Eigenschaften ist linear.
- Multikollinearität ist ausgeschlossen. Dies bedeutet, dass abhängige Variablen nicht miteinander verbunden sind.
- Homoskedastizität und Normalität von Zahlenreihen.
Die Verwendung von Korrelations- und Regressionsanalysen
Es gibt drei Hauptfälle für die Verwendung dieser Methode:
- Testen von zufälligen Beziehungen zwischen Mengen. In diesem Fall ermittelt der Forscher die Werte der Variablen und stellt fest, ob sie sich auf die Änderung der abhängigen Variablen auswirken. Zum Beispiel können Sie Menschen unterschiedliche Dosen Alkohol geben und ihren Blutdruck messen. In diesem Fall weiß der Forscher mit Sicherheit, dass der erste die Ursache für den zweiten ist und nicht umgekehrt. Mithilfe der Korrelations-Regressions-Analyse können Sie eine direkt proportionale lineare Beziehung zwischen diesen beiden Variablen erkennen und eine Formel ableiten, die diese beschreibt. In diesem Fall können Werte in völlig unterschiedlichen Maßeinheiten verglichen werden.
- Finden einer Beziehung zwischen zwei Variablen, ohne eine kausale Beziehung zu ihnen zu erweitern. In diesem Fall gibt es keinen Unterschied, welche Größe der Forscher als abhängig bezeichnet. Darüber hinaus kann sich in der Realität herausstellen, dass beide von der dritten Variablen betroffen sind, weshalb sie sich proportional ändern.
- Berechnung der Werte einer Größe anhand einer anderen. Es basiert auf einer Gleichung, in der bekannte Zahlen eingesetzt werden.
Bei der Korrelationsanalyse wird daher ein (nicht kausaler) Zusammenhang zwischen Variablen gefunden, und die Regressionsanalyse erläutert diesen Zusammenhang häufig mithilfe einer mathematischen Funktion.








